1. INTRODUCTION
In the early-1990s, when the commercial Internet was still young (!), security was taken seriously by most users. Many thought that increased security provided comfort to paranoid people while most computer professionals realized that security provided some very basic protections that we all needed? Cryptography for the masses barely existed at that time and was certainly not a topic of common discourse. By the turn of the century, of course, the Internet had grown in size and importance so as to be the provider of essential communication between billions of people around the world and is the ubiquitous tool for commerce, social interaction, and the exchange of an increasing amount of personal information — and we even have a whole form of currency named for cryptography!
Security and privacy impacts many applications, ranging from secure commerce and payments to private communications and protecting health care information. One essential aspect for secure communications is that of cryptography. But it is important to note that while cryptography is necessary for secure communications, it is not by itself sufficient. The reader is advised, then, that the topics covered here only describe the first of many steps necessary for better security in any number of situations.
This paper has two major purposes. The first is to define some of the terms and concepts behind basic cryptographic methods, and to offer a way to compare the myriad cryptographic schemes in use today. The second is to provide some real examples of cryptography in use today. (See Section A.4 for some additional commentary on this...)
DISCLAIMER: Several companies, products, and services are mentioned in this tutorial. Such mention is for example purposes only and, unless explicitly stated otherwise, should not be taken as a recommendation or endorsement by the author.
2. BASIC CONCEPTS OF CRYPTOGRAPHY
Cryptography — the science of secret writing — is an ancient art; the first documented use of cryptography in writing dates back to circa 1900 B.C. when an Egyptian scribe used non-standard hieroglyphs in an inscription. Some experts argue that cryptography appeared spontaneously sometime after writing was invented, with applications ranging from diplomatic missives to war-time battle plans. It is no surprise, then, that new forms of cryptography came soon after the widespread development of computer communications. In data and telecommunications, cryptography is necessary when communicating over any untrusted medium, which includes just about any network, particularly the Internet.
There are five primary functions of cryptography:
- Privacy/confidentiality: Ensuring that no one can read the message except the intended receiver.
- Authentication: The process of proving one's identity.
- Integrity: Assuring the receiver that the received message has not been altered in any way from the original.
- Non-repudiation: A mechanism to prove that the sender really sent this message.
- Key exchange: The method by which crypto keys are shared between sender and receiver.
In cryptography, we start with the unencrypted data, referred to as plaintext. Plaintext is encrypted into ciphertext, which will in turn (usually) be decrypted back into usable plaintext. The encryption and decryption is based upon the type of cryptography scheme being employed and some form of key. For those who like formulas, this process is sometimes written as:
C = Ek(P)
P = Dk(C)
where P = plaintext, C = ciphertext, E = the encryption method, D = the decryption method, and k = the key.
Given this, there are other functions that might be supported by crypto and other terms that one might hear:
- Forward Secrecy (aka Perfect Forward Secrecy): This feature protects past encrypted sessions from compromise even if the server holding the messages is compromised. This is accomplished by creating a different key for every session so that compromise of a single key does not threaten the entirely of the communications.
- Perfect Security: A system that is unbreakable and where the ciphertext conveys no information about the plaintext or the key. To achieve perfect security, the key has to be at least as long as the plaintext, making analysis and even brute-force attacks impossible. One-time pads are an example of such a system.
- Deniable Authentication (aka Message Repudiation): A method whereby participants in an exchange of messages can be assured in the authenticity of the messages but in such a way that senders can later plausibly deny their participation to a third-party.
In many of the descriptions below, two communicating parties will be referred to as Alice and Bob; this is the common nomenclature in the crypto field and literature to make it easier to identify the communicating parties. If there is a third and fourth party to the communication, they will be referred to as Carol and Dave, respectively. A malicious party is referred to as Mallory, an eavesdropper as Eve, and a trusted third party as Trent.
Finally, cryptography is most closely associated with the development and creation of the mathematical algorithms used to encrypt and decrypt messages, whereas cryptanalysis is the science of analyzing and breaking encryption schemes. Cryptology is the umbrella term referring to the broad study of secret writing, and encompasses both cryptography and cryptanalysis.
3. TYPES OF CRYPTOGRAPHIC ALGORITHMS
There are several ways of classifying cryptographic algorithms. For purposes of this paper, they will be categorized based on the number of keys that are employed for encryption and decryption, and further defined by their application and use. The three types of algorithms that will be discussed are (Figure 1):
- Secret Key Cryptography (SKC): Uses a single key for both encryption and decryption; also called symmetric encryption. Primarily used for privacy and confidentiality.
- Public Key Cryptography (PKC): Uses one key for encryption and another for decryption; also called asymmetric encryption. Primarily used for authentication, non-repudiation, and key exchange.
- Hash Functions: Uses a mathematical transformation to irreversibly "encrypt" information, providing a digital fingerprint. Primarily used for message integrity.
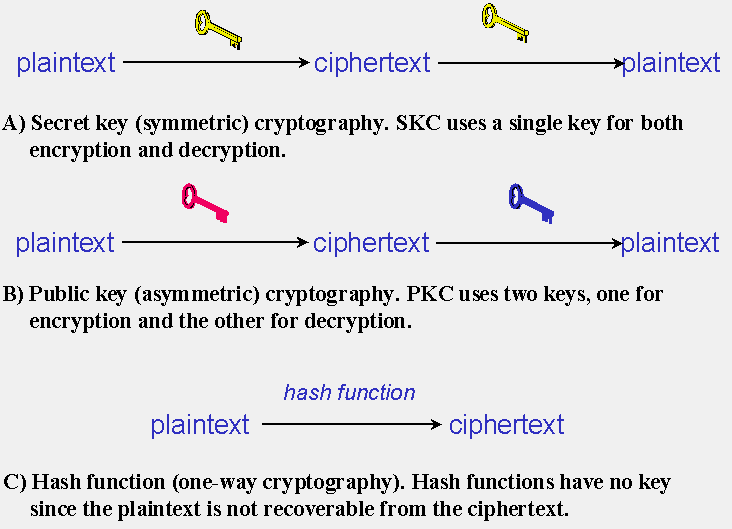 FIGURE 1: Three types of cryptography: secret key, public key, and hash function. |
3.1. Secret Key Cryptography
Secret key cryptography methods employ a single key for both encryption and decryption. As shown in Figure 1A, the sender uses the key to encrypt the plaintext and sends the ciphertext to the receiver. The receiver applies the same key to decrypt the message and recover the plaintext. Because a single key is used for both functions, secret key cryptography is also called symmetric encryption.
With this form of cryptography, it is obvious that the key must be known to both the sender and the receiver; that, in fact, is the secret. The biggest difficulty with this approach, of course, is the distribution of the key (more on that later in the discussion of public key cryptography).
Secret key cryptography schemes are generally categorized as being either stream ciphers or block ciphers.
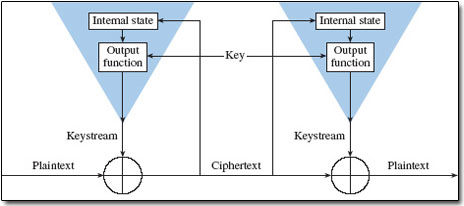
A) Self-synchronizing stream cipher. (From Schneier, 1996, Figure 9.8) 
B) Synchronous stream cipher. (From Schneier, 1996, Figure 9.6) FIGURE 2: Types of stream ciphers. |
Stream ciphers operate on a single bit (byte or computer word) at a time and implement some form of feedback mechanism so that the key is constantly changing. Stream ciphers come in several flavors but two are worth mentioning here (Figure 2). Self-synchronizing stream ciphers calculate each bit in the keystream as a function of the previous n bits in the keystream. It is termed "self-synchronizing" because the decryption process can stay synchronized with the encryption process merely by knowing how far into the n-bit keystream it is. One problem is error propagation; a garbled bit in transmission will result in n garbled bits at the receiving side. Synchronous stream ciphers generate the keystream in a fashion independent of the message stream but by using the same keystream generation function at sender and receiver. While stream ciphers do not propagate transmission errors, they are, by their nature, periodic so that the keystream will eventually repeat.
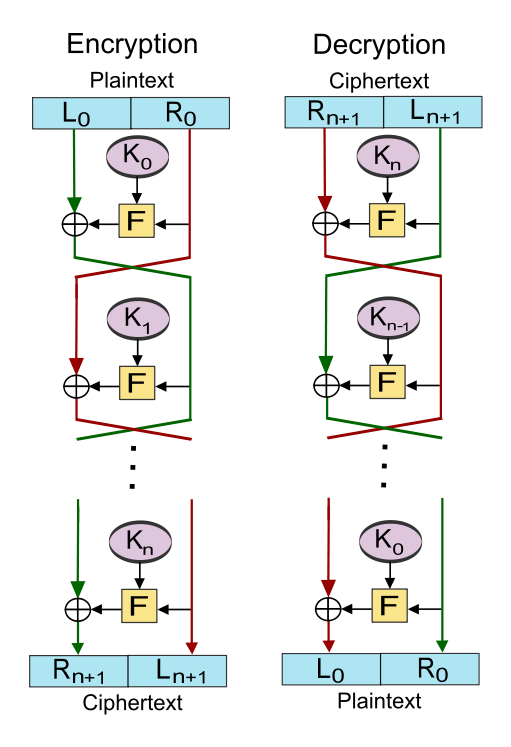
FIGURE 3: Feistel cipher. (Source: Wikimedia Commons) |
A block cipher is so-called because the scheme encrypts one fixed-size block of data at a time. In a block cipher, a given plaintext block will always encrypt to the same ciphertext when using the same key (i.e., it is deterministic) whereas the same plaintext will encrypt to different ciphertext in a stream cipher. The most common construct for block encryption algorithms is the Feistel cipher, named for cryptographer Horst Feistel (IBM). As shown in Figure 3, a Feistel cipher combines elements of substitution, permutation (transposition), and key expansion; these features create a large amount of "confusion and diffusion" (per Claude Shannon) in the cipher. One advantage of the Feistel design is that the encryption and decryption stages are similar, sometimes identical, requiring only a reversal of the key operation, thus dramatically reducing the size of the code or circuitry necessary to implement the cipher in software or hardware, respectively. One of Feistel's early papers describing this operation is "Cryptography and Computer Privacy" (Scientific American, May 1973, 228(5), 15-23).
Block ciphers can operate in one of several modes; the following are the most important:
- Electronic Codebook (ECB) mode is the simplest, most obvious application: the secret key is used to encrypt the plaintext block to form a ciphertext block. Two identical plaintext blocks, then, will always generate the same ciphertext block. ECB is susceptible to a variety of brute-force attacks (because of the fact that the same plaintext block will always encrypt to the same ciphertext), as well as deletion and insertion attacks. In addition, a single bit error in the transmission of the ciphertext results in an error in the entire block of decrypted plaintext.
- Cipher Block Chaining (CBC) mode adds a feedback mechanism to the encryption scheme; the plaintext is exclusively-ORed (XORed) with the previous ciphertext block prior to encryption so that two identical plaintext blocks will encrypt differently. While CBC protects against many brute-force, deletion, and insertion attacks, a single bit error in the ciphertext yields an entire block error in the decrypted plaintext block and a bit error in the next decrypted plaintext block.
- Cipher Feedback (CFB) mode is a block cipher implementation as a self-synchronizing stream cipher. CFB mode allows data to be encrypted in units smaller than the block size, which might be useful in some applications such as encrypting interactive terminal input. If we were using one-byte CFB mode, for example, each incoming character is placed into a shift register the same size as the block, encrypted, and the block transmitted. At the receiving side, the ciphertext is decrypted and the extra bits in the block (i.e., everything above and beyond the one byte) are discarded. CFB mode generates a keystream based upon the previous ciphertext (the initial key comes from an Initialization Vector [IV]). In this mode, a single bit error in the ciphertext affects both this block and the following one.
- Output Feedback (OFB) mode is a block cipher implementation conceptually similar to a synchronous stream cipher. OFB prevents the same plaintext block from generating the same ciphertext block by using an internal feedback mechanism that generates the keystream independently of both the plaintext and ciphertext bitstreams. In OFB, a single bit error in ciphertext yields a single bit error in the decrypted plaintext.
- Counter (CTR) mode is a relatively modern addition to block ciphers. Like CFB and OFB, CTR mode operates on the blocks as in a stream cipher; like ECB, CTR mode operates on the blocks independently. Unlike ECB, however, CTR uses different key inputs to different blocks so that two identical blocks of plaintext will not result in the same ciphertext. Finally, each block of ciphertext has specific location within the encrypted message. CTR mode, then, allows blocks to be processed in parallel — thus offering performance advantages when parallel processing and multiple processors are available — but is not susceptible to ECB's brute-force, deletion, and insertion attacks.
A good overview of these different modes can be found at CRYPTO-IT.
Secret key cryptography algorithms in use today — or, at least, important today even if not in use — include:
-
Data Encryption Standard (DES): One of the most well-known and well-studied SKC schemes, DES was designed by IBM in the 1970s and adopted by the National Bureau of Standards (NBS) [now the National Institute of Standards and Technology (NIST)] in 1977 for commercial and unclassified government applications. DES is a Feistel block-cipher employing a 56-bit key that operates on 64-bit blocks. DES has a complex set of rules and transformations that were designed specifically to yield fast hardware implementations and slow software implementations, although this latter point is not significant today since the speed of computer processors is several orders of magnitude faster today than even twenty years ago. DES was based somewhat on an earlier cipher from Feistel called Lucifer which, some sources report, had a 112-bit key. This was rejected, partially in order to fit the algorithm onto a single chip and partially because of the National Security Agency (NSA). The NSA also proposed a number of tweaks to DES that many thought were introduced in order to weaken the cipher; analysis in the 1990s, however, showed that the NSA suggestions actually strengthened DES, including the removal of a mathematical back door by a change to the design of the S-box (see "The Legacy of DES" by Bruce Schneier [2004]). In April 2021, the NSA declassified a fascinating historical paper titled "NSA Comes Out of the Closet: The Debate over Public Cryptography in the Inman Era" that appeared in Cryptologic Quarterly, Spring 1996.
DES was defined in American National Standard X3.92 and three Federal Information Processing Standards (FIPS), all withdrawn in 2005:
- FIPS PUB 46-3: DES (Archived file)
- FIPS PUB 74: Guidelines for Implementing and Using the NBS Data Encryption Standard
- FIPS PUB 81: DES Modes of Operation
Information about vulnerabilities of DES can be obtained from the Electronic Frontier Foundation.
Two important variants that strengthen DES are:
-
Triple-DES (3DES): A variant of DES that employs up to three 56-bit keys and makes three encryption/decryption passes over the block; 3DES is also described in FIPS PUB 46-3 and was an interim replacement to DES in the late-1990s and early-2000s.
-
DESX: A variant devised by Ron Rivest. By combining 64 additional key bits to the plaintext prior to encryption, effectively increases the keylength to 120 bits.
More detail about DES, 3DES, and DESX can be found below in Section 5.4.
-
Advanced Encryption Standard (AES): In 1997, NIST initiated a very public, 4-1/2 year process to develop a new secure cryptosystem for U.S. government applications (as opposed to the very closed process in the adoption of DES 25 years earlier). The result, the Advanced Encryption Standard, became the official successor to DES in December 2001. AES uses an SKC scheme called Rijndael, a block cipher designed by Belgian cryptographers Joan Daemen and Vincent Rijmen. The algorithm can use a variable block length and key length; the latest specification allowed any combination of keys lengths of 128, 192, or 256 bits and blocks of length 128, 192, or 256 bits. NIST initially selected Rijndael in October 2000 and formal adoption as the AES standard came in December 2001. FIPS PUB 197 describes a 128-bit block cipher employing a 128-, 192-, or 256-bit key. AES is also part of the NESSIE approved suite of protocols. (See also the entries for CRYPTEC and NESSIE Projects in Table 3.)
The AES process and Rijndael algorithm are described in more detail below in Section 5.9.
-
CAST-128/256: CAST-128 (aka CAST5), described in Request for Comments (RFC) 2144, is a DES-like substitution-permutation crypto algorithm, employing a 128-bit key operating on a 64-bit block. CAST-256 (aka CAST6), described in RFC 2612, is an extension of CAST-128, using a 128-bit block size and a variable length (128, 160, 192, 224, or 256 bit) key. CAST is named for its developers, Carlisle Adams and Stafford Tavares, and is available internationally. CAST-256 was one of the Round 1 algorithms in the AES process.
-
International Data Encryption Algorithm (IDEA): Secret-key cryptosystem written by Xuejia Lai and James Massey, in 1992 and patented by Ascom; a 64-bit SKC block cipher using a 128-bit key.
-
Rivest Ciphers (aka Ron's Code): Named for Ron Rivest, a series of SKC algorithms.
-
RC1: Designed on paper but never implemented.
-
RC2: A 64-bit block cipher using variable-sized keys designed to replace DES. It's code has not been made public although many companies have licensed RC2 for use in their products. Described in RFC 2268.
-
RC3: Found to be breakable during development.
-
RC4: A stream cipher using variable-sized keys; it is widely used in commercial cryptography products. An update to RC4, called Spritz (see also this article), was designed by Rivest and Jacob Schuldt. More detail about RC4 (and a little about Spritz) can be found below in Section 5.13.
-
RC5: A block-cipher supporting a variety of block sizes (32, 64, or 128 bits), key sizes, and number of encryption passes over the data. Described in RFC 2040.
-
RC6: A 128-bit block cipher based upon, and an improvement over, RC5; RC6 was one of the AES Round 2 algorithms.
-
-
Blowfish: A symmetric 64-bit block cipher invented by Bruce Schneier; optimized for 32-bit processors with large data caches, it is significantly faster than DES on a Pentium/PowerPC-class machine. Key lengths can vary from 32 to 448 bits in length. Blowfish, available freely and intended as a substitute for DES or IDEA, is in use in a large number of products.
-
Twofish: A 128-bit block cipher using 128-, 192-, or 256-bit keys. Designed to be highly secure and highly flexible, well-suited for large microprocessors, 8-bit smart card microprocessors, and dedicated hardware. Designed by a team led by Bruce Schneier and was one of the Round 2 algorithms in the AES process.
-
Threefish: A large block cipher, supporting 256-, 512-, and 1024-bit blocks and a key size that matches the block size; by design, the block/key size can grow in increments of 128 bits. Threefish only uses XOR operations, addition, and rotations of 64-bit words; the design philosophy is that an algorithm employing many computationally simple rounds is more secure than one employing highly complex — albeit fewer — rounds. The specification for Threefish is part of the Skein Hash Function Family documentation.
-
Anubis: Anubis is a block cipher, co-designed by Vincent Rijmen who was one of the designers of Rijndael. Anubis is a block cipher, performing substitution-permutation operations on 128-bit blocks and employing keys of length 128 to 3200 bits (in 32-bit increments). Anubis works very much like Rijndael. Although submitted to the NESSIE project, it did not make the final cut for inclusion.
-
ARIA: A 128-bit block cipher employing 128-, 192-, and 256-bit keys to encrypt 128-bit blocks in 12, 14, and 16 rounds, depending on the key size. Developed by large group of researchers from academic institutions, research institutes, and federal agencies in South Korea in 2003, and subsequently named a national standard. Described in RFC 5794.
-
Camellia: A secret-key, block-cipher crypto algorithm developed jointly by Nippon Telegraph and Telephone (NTT) Corp. and Mitsubishi Electric Corporation (MEC) in 2000. Camellia has some characteristics in common with AES: a 128-bit block size, support for 128-, 192-, and 256-bit key lengths, and suitability for both software and hardware implementations on common 32-bit processors as well as 8-bit processors (e.g., smart cards, cryptographic hardware, and embedded systems). Also described in RFC 3713. Camellia's application in IPsec is described in RFC 4312 and application in OpenPGP in RFC 9580. Camellia is part of the NESSIE suite of protocols.
-
CLEFIA: Described in RFC 6114, CLEFIA is a 128-bit block cipher employing key lengths of 128, 192, and 256 bits (which is compatible with AES). The CLEFIA algorithm was first published in 2007 by Sony Corporation. CLEFIA is one of the new-generation lightweight block cipher algorithms designed after AES, offering high performance in software and hardware as well as a lightweight implementation in hardware.
-
FFX-A2 and FFX-A10: FFX (Format-preserving, Feistel-based encryption) is a type of Format Preserving Encryption (FPE) scheme that is designed so that the ciphertext has the same format as the plaintext. FPE schemes are used for such purposes as encrypting social security numbers, credit card numbers, limited size protocol traffic, etc.; this means that an encrypted social security number, for example, would still be a nine-digit string. FFX can theoretically encrypt strings of arbitrary length, although it is intended for message sizes smaller than that of AES-128 (2128 points). The FFX version 1.1 specification describes FFX-A2 and FFX-A10, which are intended for 8-128 bit binary strings or 4-36 digit decimal strings.
-
GSM (Global System for Mobile Communications, originally Groupe Spécial Mobile) encryption: GSM mobile phone systems use several stream ciphers for over-the-air communication privacy. A5/1 was developed in 1987 for use in Europe and the U.S. A5/2, developed in 1989, is a weaker algorithm and intended for use outside of Europe and the U.S. Significant flaws were found in both ciphers after the "secret" specifications were leaked in 1994, however, and A5/2 has been withdrawn from use. The newest version, A5/3, employs the KASUMI block cipher. NOTE: Unfortunately, although A5/1 has been repeatedly "broken" (e.g., see "Secret code protecting cellphone calls set loose" [2009] and "Cellphone snooping now easier and cheaper than ever" [2011]), this encryption scheme remains in widespread use, even in 3G and 4G mobile phone networks. Use of this scheme is reportedly one of the reasons that the National Security Agency (NSA) can easily decode voice and data calls over mobile phone networks.
-
GPRS (General Packet Radio Service) encryption: GSM mobile phone systems use GPRS for data applications, and GPRS uses a number of encryption methods, offering different levels of data protection. GEA/0 offers no encryption at all. GEA/1 and GEA/2 are proprietary stream ciphers, employing a 64-bit key and a 96-bit or 128-bit state, respectively. GEA/1 and GEA/2 are most widely used by network service providers today although both have been reportedly broken. GEA/3 is a 128-bit block cipher employing a 64-bit key that is used by some carriers; GEA/4 is a 128-bit clock cipher with a 128-bit key, but is not yet deployed.
-
KASUMI: A block cipher using a 128-bit key that is part of the Third-Generation Partnership Project (3gpp), formerly known as the Universal Mobile Telecommunications System (UMTS). KASUMI is the intended confidentiality and integrity algorithm for both message content and signaling data for emerging mobile communications systems.
-
KCipher-2: Described in RFC 7008, KCipher-2 is a stream cipher with a 128-bit key and a 128-bit initialization vector. Using simple arithmetic operations, the algorithms offers fast encryption and decryption by use of efficient implementations. KCipher-2 has been used for industrial applications, especially for mobile health monitoring and diagnostic services in Japan.
-
KHAZAD: KHAZAD is a so-called legacy block cipher, operating on 64-bit blocks à la older block ciphers such as DES and IDEA. KHAZAD uses eight rounds of substitution and permutation, with a 128-bit key.
-
KLEIN: Designed in 2011, KLEIN is a lightweight, 64-bit block cipher supporting 64-, 80- and 96-bit keys. KLEIN is designed for highly resource constrained devices such as wireless sensors and RFID tags.
-
Light Encryption Device (LED): Designed in 2011, LED is a lightweight, 64-bit block cipher supporting 64- and 128-bit keys. LED is designed for RFID tags, sensor networks, and other applications with devices constrained by memory or compute power.
-
MARS: MARS is a block cipher developed by IBM and was one of the five finalists in the AES development process. MARS employs 128-bit blocks and a variable key length from 128 to 448 bits. The MARS document stresses the ability of the algorithm's design for high speed, high security, and the ability to efficiently and effectively implement the scheme on a wide range of computing devices.
-
MISTY1: Developed at Mitsubishi Electric Corp., a block cipher using a 128-bit key and 64-bit blocks, and a variable number of rounds. Designed for hardware and software implementations, and is resistant to differential and linear cryptanalysis. Described in RFC 2994, MISTY1 is part of the NESSIE suite.
-
Salsa and ChaCha: Salsa20 is a stream cipher proposed for the eSTREAM project by Daniel Bernstein. Salsa20 uses a pseudorandom function based on 32-bit (whole word) addition, bitwise addition (XOR), and rotation operations, aka add-rotate-xor (ARX) operations. Salsa20 uses a 256-bit key although a 128-bit key variant also exists. In 2008, Bernstein published ChaCha, a new family of ciphers related to Salsa20. ChaCha20, originally defined in RFC 7539 (now obsoleted), is employed (with the Poly1305 authenticator) in Internet Engineering Task Force (IETF) protocols, most notably for IPsec and Internet Key Exchange (IKE), per RFC 7634, and Transaction Layer Security (TLS), per RFC 7905. In 2014, Google adopted ChaCha20/Poly1305 for use in OpenSSL, and they are also a part of OpenSSH. RFC 8439 replaces RFC 7539, and provides an implementation guide for both the ChaCha20 cipher and Poly1305 message authentication code, as well as the combined CHACHA20-POLY1305 Authenticated-Encryption with Associated-Data (AEAD) algorithm.
-
Secure and Fast Encryption Routine (SAFER): A series of block ciphers designed by James Massey for implementation in software and employing a 64-bit block. SAFER K-64, published in 1993, used a 64-bit key and SAFER K-128, published in 1994, employed a 128-bit key. After weaknesses were found, new versions were released called SAFER SK-40, SK-64, and SK-128, using 40-, 64-, and 128-bit keys, respectively. SAFER+ (1998) used a 128-bit block and was an unsuccessful candidate for the AES project; SAFER++ (2000) was submitted to the NESSIE project.
-
SEED: A block cipher using 128-bit blocks and 128-bit keys. Developed by the Korea Information Security Agency (KISA) and adopted as a national standard encryption algorithm in South Korea. Also described in RFC 4269.
-
Serpent: Serpent is another of the AES finalist algorithms. Serpent supports 128-, 192-, or 256-bit keys and a block size of 128 bits, and is a 32-round substitution–permutation network operating on a block of four 32-bit words. The Serpent developers opted for a high security margin in the design of the algorithm; they determined that 16 rounds would be sufficient against known attacks but require 32 rounds in an attempt to future-proof the algorithm.
-
SHACAL: SHACAL is a pair of block ciphers based upon the Secure Hash Algorithm (SHA) and the fact that SHA is, at heart, a compression algorithm. As a hash function, SHA repeatedly calls on a compression scheme to alter the state of the data blocks. While SHA (like other hash functions) is irreversible, the compression function can be used for encryption by maintaining appropriate state information. SHACAL-1 is based upon SHA-1 and uses a 160-bit block size while SHACAL-2 is based upon SHA-256 and employs a 256-bit block size; both support key sizes from 128 to 512 bits. SHACAL-2 is one of the NESSIE block ciphers.
-
Simon and Speck: Simon and Speck are a pair of lightweight block ciphers proposed by the NSA in 2013, designed for highly constrained software or hardware environments. (E.g., per the specification, AES requires 2400 gate equivalents and these ciphers require less than 2000.) While both cipher families perform well in both hardware and software, Simon has been optimized for high performance on hardware devices and Speck for performance in software. Both are Feistel ciphers and support ten combinations of block and key size:
-
Skipjack: SKC scheme proposed, along with the Clipper chip, as part of the never-implemented Capstone project. Although the details of the algorithm were never made public, Skipjack was a block cipher using an 80-bit key and 32 iteration cycles per 64-bit block. Capstone, proposed by NIST and the NSA as a standard for public and government use, met with great resistance by the crypto community largely because the design of Skipjack was classified (coupled with the key escrow requirement of the Clipper chip).
-
SM4: Formerly called SMS4, SM4 is a 128-bit block cipher using 128-bit keys and 32 rounds to process a block. Declassified in 2006, SM4 is used in the Chinese National Standard for Wireless Local Area Network (LAN) Authentication and Privacy Infrastructure (WAPI). SM4 had been a proposed cipher for the Institute of Electrical and Electronics Engineers (IEEE) 802.11i standard on security mechanisms for wireless LANs, but has yet to be accepted by the IEEE or International Organization for Standardization (ISO). SM4 is described in SMS4 Encryption Algorithm for Wireless Networks (translated by Whitfield Diffie and George Ledin, 2008) and at the SM4 (cipher) page. SM4 is issued by the Chinese State Cryptographic Authority as GM/T 0002-2012: SM4 (2012).
-
Tiny Encryption Algorithm (TEA): A family of block ciphers developed by Roger Needham and David Wheeler. TEA was originally developed in 1994, and employed a 128-bit key, 64-bit block, and 64 rounds of operation. To correct certain weaknesses in TEA, eXtended TEA (XTEA), aka Block TEA, was released in 1997. To correct weaknesses in XTEA and add versatility, Corrected Block TEA (XXTEA) was published in 1998. XXTEA also uses a 128-bit key, but block size can be any multiple of 32-bit words (with a minimum block size of 64 bits, or two words) and the number of rounds is a function of the block size (~52+6*words), as shown in Table 1.
-
TWINE: Designed by engineers at NEC in 2011, TWINE is a lightweight, 64-bit block cipher supporting 80- and 128-bit keys. TWINE's design goals included maintaining a small footprint in a hardware implementation (i.e., fewer than 2,000 gate equivalents) and small memory consumption in a software implementation.
| Block Size 2n |
Key Size mn |
Word Size n |
Key Words m |
Rounds T |
|---|---|---|---|---|
| 32 | 64 | 16 | 4 | 32 |
| 48 | 72 96 |
24 | 3 4 |
36 36 |
| 64 | 96 128 |
32 | 3 4 |
42 44 |
| 96 | 96 144 |
48 | 2 3 |
52 54 |
| 128 | 128 192 256 |
64 | 2 3 4 |
68 69 72 |
Although not an SKC scheme, check out Section 5.17 about Shamir's Secret Sharing (SSS).
There are several other references that describe interesting algorithms and even SKC codes dating back decades. Two that leap to mind are the Crypto Museum's Crypto List and John J.G. Savard's (albeit old) A Cryptographic Compendium page.
3.2. Public Key Cryptography
Public key cryptography has been said to be the most significant new development in cryptography in the last 300-400 years. Modern PKC was first described publicly by Stanford University professor Martin Hellman and graduate student Whitfield Diffie in 1976. Their paper described a two-key crypto system in which two parties could engage in a secure communication over a non-secure communications channel without having to share a secret key.
PKC depends upon the existence of so-called one-way functions, or mathematical functions that are easy to compute whereas their inverse function is relatively difficult to compute. Let me give you two simple examples:
- Multiplication vs. factorization: Suppose you have two prime numbers, 3 and 7, and you need to calculate the product; it should take almost no time to calculate that value, which is 21. Now suppose, instead, that you have a number that is a product of two primes, 21, and you need to determine those prime factors. You will eventually come up with the solution but whereas calculating the product took milliseconds, factoring will take longer. The problem becomes much harder if we start with primes that have, say, 400 digits or so, because the product will have ~800 digits.
- Exponentiation vs. logarithms: Suppose you take the number 3 to the 6th power; again, it is relatively easy to calculate 36 = 729. But if you start with the number 729 and need to determine the two integers, x and y so that logx 729 = y, it will take longer to find the two values.
While the examples above are trivial, they do represent two of the functional pairs that are used with PKC; namely, the ease of multiplication and exponentiation versus the relative difficulty of factoring and calculating logarithms, respectively. The mathematical "trick" in PKC is to find a trap door in the one-way function so that the inverse calculation becomes easy given knowledge of some item of information.
Generic PKC employs two keys that are mathematically related. One of the keys is designated the public key and may be advertised as widely as the owner wants. The other key is designated the private key and is never revealed to another party. Great care must be taken to protect the private key since the public key is derived from it. That said, either key can be used to encrypt the plaintext and the other key then used to decrypt the ciphertext. The important point here is that it does not matter which key is applied first, but that both keys are required for the process to work (Figure 1B). Because a pair of keys are required, this approach is also called asymmetric cryptography.
It is straight-forward to send messages under this scheme. Suppose Alice wants to send Bob a message. Alice encrypts some information using Bob's public key; Bob decrypts the ciphertext using his own private key. This method could be also used to prove who sent a message — Alice, for example, could encrypt some plaintext with her private key; when Bob decrypts that block using Alice's public key, he knows that Alice sent the message (authentication) and Alice cannot deny having sent the message (non-repudiation).
Public key cryptography algorithms that are in use today for key exchange or digital signatures include:
-
RSA: The first, and still most common, PKC implementation, named for the three MIT mathematicians who developed it — Ronald Rivest, Adi Shamir, and Leonard Adleman. RSA today is used in hundreds of software products and can be used for key exchange, digital signatures, or encryption of small blocks of data. RSA uses a variable size encryption block and a variable size key. The key-pair is derived from a very large number, n, that is the product of two prime numbers chosen according to special rules; these primes may be 100 or more digits in length each, yielding an n with roughly twice as many digits as the prime factors. The public key information includes n and a derivative of one of the factors of n; an attacker cannot determine the prime factors of n (and, therefore, the private key) from this information alone and that is what makes the RSA algorithm so secure. (Some descriptions of PKC erroneously state that RSA's safety is due to the difficulty in factoring large prime numbers. In fact, large prime numbers, like small prime numbers, only have two factors!) The ability for computers to factor large numbers, and therefore attack schemes such as RSA, is rapidly improving and systems today can find the prime factors of numbers with more than 200 digits. Nevertheless, if a large number is created from two prime factors that are roughly the same size, there is no known factorization algorithm that will solve the problem in a reasonable amount of time; a 2005 test to factor a 200-digit number took 1.5 years and over 50 years of compute time. In 2009, Kleinjung et al. reported that factoring a 768-bit (232-digit) RSA-768 modulus utilizing hundreds of systems took two years and they estimated that a 1024-bit RSA modulus would take about a thousand times as long. Even so, they suggested that 1024-bit RSA be phased out by 2013. (See the Wikipedia article on integer factorization.) Regardless, one presumed protection of RSA is that users can easily increase the key size to always stay ahead of the computer processing curve. As an aside, the patent for RSA expired in September 2000 which does not appear to have affected RSA's popularity one way or the other. A detailed example of RSA is presented below in Section 5.3.
-
Diffie-Hellman: After the RSA algorithm was published, Diffie and Hellman came up with their own algorithm. Diffie-Hellman is used for secret-key key exchange only, and not for authentication or digital signatures. More detail about Diffie-Hellman can be found below in Section 5.2.
-
Digital Signature Algorithm (DSA): The algorithm specified in NIST's Digital Signature Standard (DSS), provides digital signature capability for the authentication of messages. Described in FIPS PUB 186-4.
-
ElGamal: Designed by Taher Elgamal, ElGamal is a PKC system similar to Diffie-Hellman and used for key exchange. ElGamal is used in some later version of Pretty Good Privacy (PGP) as well as GNU Privacy Guard (GPG) and other cryptosystems.
-
Elliptic Curve Cryptography (ECC): A PKC algorithm based upon elliptic curves. ECC can offer levels of security with small keys comparable to RSA and other PKC methods. It was designed for devices with limited compute power and/or memory, such as smartcards and PDAs. More detail about ECC can be found below in Section 5.8. Other references include the Elliptic Curve Cryptography page and the Online ECC Tutorial page, both from Certicom. See also RFC 6090 for a review of fundamental ECC algorithms and The Elliptic Curve Digital Signature Algorithm (ECDSA) for details about the use of ECC for digital signatures.
-
Identity-Based Encryption (IBE): IBE is a novel scheme first proposed by Adi Shamir in 1984. It is a PKC-based key authentication system where the public key can be derived from some unique information based upon the user's identity, allowing two users to exchange encrypted messages without having an a priori relationship. In 2001, Dan Boneh (Stanford) and Matt Franklin (U.C., Davis) developed a practical implementation of IBE based on elliptic curves and a mathematical construct called the Weil Pairing. In that year, Clifford Cocks (GCHQ) also described another IBE solution based on quadratic residues in composite groups. RFC 5091: Identity-Based Cryptography Standard (IBCS) #1 describes an implementation of IBE using Boneh-Franklin (BF) and Boneh-Boyen (BB1) Identity-based Encryption. More detail about Identity-Based Encryption can be found below in Section 5.16.
-
Public Key Cryptography Standards (PKCS): A set of interoperable standards and guidelines for public key cryptography, designed by RSA Data Security Inc. (These documents are no longer easily available; all links in this section are from archive.org.)
- PKCS #1: RSA Cryptography Standard (Also RFC 8017)
- PKCS #2: Incorporated into PKCS #1.
- PKCS #3: Diffie-Hellman Key-Agreement Standard
- PKCS #4: Incorporated into PKCS #1.
- PKCS #5: Password-Based Cryptography Standard (PKCS #5 V2.1 is also RFC 8018)
- PKCS #6: Extended-Certificate Syntax Standard (being phased out in favor of X.509v3)
- PKCS #7: Cryptographic Message Syntax Standard (Also RFC 2315)
- PKCS #8: Private-Key Information Syntax Standard (Also RFC 5958)
- PKCS #9: Selected Attribute Types (Also RFC 2985)
- PKCS #10: Certification Request Syntax Standard (Also RFC 2986)
- PKCS #11: Cryptographic Token Interface Standard
- PKCS #12: Personal Information Exchange Syntax Standard (Also RFC 7292)
- PKCS #13: Elliptic Curve Cryptography Standard
- PKCS #14: Pseudorandom Number Generation Standard is no longer available
- PKCS #15: Cryptographic Token Information Format Standard
-
Cramer-Shoup: A public key cryptosystem proposed by R. Cramer and V. Shoup of IBM in 1998.
-
Key Exchange Algorithm (KEA): A variation on Diffie-Hellman; proposed as the key exchange method for the NIST/NSA Capstone project.
-
LUC: A public key cryptosystem designed by P.J. Smith and based on Lucas sequences. Can be used for encryption and signatures, using integer factoring.
-
McEliece: A public key cryptosystem based on algebraic coding theory.
For additional information on PKC algorithms, see "Public Key Encryption" (Chapter 8) in Handbook of Applied Cryptography, by A. Menezes, P. van Oorschot, and S. Vanstone (CRC Press, 1996).
A digression: Who invented PKC? I tried to be careful in the first paragraph of this section to state that Diffie and Hellman "first described publicly" a PKC scheme. Although I have categorized PKC as a two-key system, that has been merely for convenience; the real criteria for a PKC scheme is that it allows two parties to exchange a secret even though the communication with the shared secret might be overheard. There seems to be no question that Diffie and Hellman were first to publish; their method is described in the classic paper, "New Directions in Cryptography," published in the November 1976 issue of IEEE Transactions on Information Theory (IT-22(6), 644-654). As shown in Section 5.2, Diffie-Hellman uses the idea that finding logarithms is relatively harder than performing exponentiation. And, indeed, it is the precursor to modern PKC which does employ two keys. Rivest, Shamir, and Adleman described an implementation that extended this idea in their paper, "A Method for Obtaining Digital Signatures and Public Key Cryptosystems," published in the February 1978 issue of the Communications of the ACM (CACM), (21(2), 120-126). Their method, of course, is based upon the relative ease of finding the product of two large prime numbers compared to finding the prime factors of a large number.
Diffie and Hellman (and other sources) credit Ralph Merkle with first describing a public key distribution system that allows two parties to share a secret, although it was not a two-key system, per se. A Merkle Puzzle works where Alice creates a large number of encrypted keys, sends them all to Bob so that Bob chooses one at random and then lets Alice know which he has selected. An eavesdropper (Eve) will see all of the keys but can't learn which key Bob has selected (because he has encrypted the response with the chosen key). In this case, Eve's effort to break in is the square of the effort of Bob to choose a key. While this difference may be small it is often sufficient. Merkle apparently took a computer science course at UC Berkeley in 1974 and described his method, but had difficulty making people understand it; frustrated, he dropped the course. Meanwhile, he submitted the paper "Secure Communication Over Insecure Channels," which was published in the CACM in April 1978; Rivest et al.'s paper even makes reference to it. Merkle's method certainly wasn't published first, but he is often credited to have had the idea first.
An interesting question, maybe, but who really knows? For some time, it was a quiet secret that a team at the UK's Government Communications Headquarters (GCHQ) had first developed PKC in the early 1970s. Because of the nature of the work, GCHQ kept the original memos classified. In 1997, however, the GCHQ changed their posture when they realized that there was nothing to gain by continued silence. Documents show that a GCHQ mathematician named James Ellis started research into the key distribution problem in 1969 and that by 1975, James Ellis, Clifford Cocks, and Malcolm Williamson had worked out all of the fundamental details of PKC, yet couldn't talk about their work. (They were, of course, barred from challenging the RSA patent!) By 1999, Ellis, Cocks, and Williamson began to get their due credit in a break-through article in WIRED Magazine. And the National Security Agency (NSA) claims to have knowledge of this type of algorithm as early as 1966. For some additional insight on who knew what when, see Steve Bellovin's "The Prehistory of Public Key Cryptography."
3.3. Hash Functions
Hash functions, also called message digests and one-way encryption, are algorithms that, in essence, use no key (Figure 1C). Instead, a fixed-length hash value is computed based upon the plaintext that makes it impossible for either the contents or length of the plaintext to be recovered. Hash algorithms are typically used to provide a digital fingerprint of a file's contents, often used to ensure that the file has not been altered by an intruder or virus. Hash functions are also commonly employed by many operating systems to encrypt passwords. Hash functions, then, provide a mechanism to ensure the integrity of a file.
Hash functions are also designed so that small changes in the input produce significant differences in the hash value, for example:
Hash string 1: The quick brown fox jumps over the lazy dog
Hash string 2: The quick brown fox jumps over the lazy dog.
MD5 [hash string 1] = 37c4b87edffc5d198ff5a185cee7ee09
MD5 [hash string 2] = 0d7006cd055e94cf614587e1d2ae0c8e
SHA1 [hash string 1] = be417768b5c3c5c1d9bcb2e7c119196dd76b5570
SHA1 [hash string 2] = 9c04cd6372077e9b11f70ca111c9807dc7137e4b
RIPEMD160 [hash string 1] = ee061f0400729d0095695da9e2c95168326610ff
RIPEMD160 [hash string 2] = 99b90925a0116c302984211dbe25b5343be9059e
Let me reiterate that hashes are one-way encryption. You cannot take a hash and "decrypt" it to find the original string that created it, despite the many web sites that claim or suggest otherwise, such as CrackStation, Hashes.com, MD5 Online, md5thiscracker, OnlineHashCrack, and RainbowCrack.Note that these sites search databases and/or use rainbow tables to find a suitable string that produces the hash in question but one can't definitively guarantee what string originally produced the hash. This is an important distinction. Suppose that you want to crack someone's password, where the hash of the password is stored on the server. Indeed, all you then need is a string that produces the correct hash and you're in! However, you cannot prove that you have discovered the user's password, only a "duplicate key."
Hash algorithms in common use today include:
-
Message Digest (MD) algorithms: A series of byte-oriented algorithms that produce a 128-bit hash value from an arbitrary-length message.
-
MD2 (RFC 1319): Designed for systems with limited memory, such as smart cards. (MD2 has been relegated to historical status, per RFC 6149.)
-
MD4 (RFC 1320): Developed by Rivest, similar to MD2 but designed specifically for fast processing in software. (MD4 has been relegated to historical status, per RFC 6150.)
-
MD5 (RFC 1321): Also developed by Rivest after potential weaknesses were reported in MD4; this scheme is similar to MD4 but is slower because more manipulation is made to the original data. MD5 has been implemented in a large number of products although several weaknesses in the algorithm were demonstrated by German cryptographer Hans Dobbertin in 1996 ("Cryptanalysis of MD5 Compress"). (Updated security considerations for MD5 can be found in RFC 6151.)
-
-
Secure Hash Algorithm (SHA): Algorithm for NIST's Secure Hash Standard (SHS), described in FIPS PUB 180-4 The status of NIST hash algorithms can be found on their "Policy on Hash Functions" page.
SHA-1 produces a 160-bit hash value and was originally published as FIPS PUB 180-1 and RFC 3174. SHA-1 was deprecated by NIST as of the end of 2013 although it is still widely used.
SHA-2, originally described in FIPS PUB 180-2 and eventually replaced by FIPS PUB 180-3 (and FIPS PUB 180-4), comprises five algorithms in the SHS: SHA-1 plus SHA-224, SHA-256, SHA-384, and SHA-512 which can produce hash values that are 224, 256, 384, or 512 bits in length, respectively. SHA-2 recommends use of SHA-1, SHA-224, and SHA-256 for messages less than 264 bits in length, and employs a 512 bit block size; SHA-384 and SHA-512 are recommended for messages less than 2128 bits in length, and employs a 1,024 bit block size. FIPS PUB 180-4 also introduces the concept of a truncated hash in SHA-512/t, a generic name referring to a hash value based upon the SHA-512 algorithm that has been truncated to t bits; SHA-512/224 and SHA-512/256 are specifically described. SHA-224, -256, -384, and -512 are also described in RFC 4634.
SHA-3 is the current SHS algorithm. Although there had not been any successful attacks on SHA-2, NIST decided that having an alternative to SHA-2 using a different algorithm would be prudent. In 2007, they launched a SHA-3 Competition to find that alternative; a list of submissions can be found at The SHA-3 Zoo. In 2012, NIST announced that after reviewing 64 submissions, the winner was Keccak (pronounced "catch-ack"), a family of hash algorithms based on sponge functions. The NIST version can support hash output sizes of 256 and 512 bits.
-
RIPEMD: A series of message digests that initially came from the RIPE (RACE Integrity Primitives Evaluation) project. RIPEMD-160 was designed by Hans Dobbertin, Antoon Bosselaers, and Bart Preneel, and optimized for 32-bit processors to replace the then-current 128-bit hash functions. Other versions include RIPEMD-256, RIPEMD-320, and RIPEMD-128.
-
eD2k: Named for the EDonkey2000 Network (eD2K), the eD2k hash is a root hash of an MD4 hash list of a given file. A root hash is used on peer-to-peer file transfer networks, where a file is broken into chunks; each chunk has its own MD4 hash associated with it and the server maintains a file that contains the hash list of all of the chunks. The root hash is the hash of the hash list file.
-
HAVAL (HAsh of VAriable Length): Designed by Y. Zheng, J. Pieprzyk and J. Seberry, a hash algorithm with many levels of security. HAVAL can create hash values that are 128, 160, 192, 224, or 256 bits in length. More details can be found in "HAVAL - A one-way hashing algorithm with variable length output" by Zheng, Pieprzyk, and Seberry (AUSCRYPT '92).
-
The Skein Hash Function Family: The Skein Hash Function Family was proposed to NIST in their 2010 hash function competition. Skein is fast due to using just a few simple computational primitives, secure, and very flexible — per the specification, it can be used as a straight-forward hash, MAC, HMAC, digital signature hash, key derivation mechanism, stream cipher, or pseudo-random number generator. Skein supports internal state sizes of 256, 512 and 1024 bits, and arbitrary output lengths.
-
SM3: SM3 is a 256-bit hash function operating on 512-bit input blocks. Part of a Chinese National Standard, SM3 is issued by the Chinese State Cryptographic Authority as GM/T 0004-2012: SM3 cryptographic hash algorithm (2012) and GB/T 32905-2016: Information security techniques—SM3 cryptographic hash algorithm (2016). More information can also be found at the SM3 (hash function) page.
-
Tiger: Designed by Ross Anderson and Eli Biham, Tiger is designed to be secure, run efficiently on 64-bit processors, and easily replace MD4, MD5, SHA and SHA-1 in other applications. Tiger/192 produces a 192-bit output and is compatible with 64-bit architectures; Tiger/128 and Tiger/160 produce a hash of length 128 and 160 bits, respectively, to provide compatibility with the other hash functions mentioned above.
-
Whirlpool: Designed by V. Rijmen (co-inventor of Rijndael) and P.S.L.M. Barreto, Whirlpool is one of two hash functions endorsed by the NESSIE competition (the other being SHA). Whirlpool operates on messages less than 2256 bits in length and produces a message digest of 512 bits. The design of this hash function is very different than that of MD5 and SHA-1, making it immune to the types of attacks that succeeded on those hashes.
Readers might be interested in HashCalc, a Windows-based program that calculates hash values using a dozen algorithms, including MD5, SHA-1 and several variants, RIPEMD-160, and Tiger. Command line utilities that calculate hash values include sha_verify by Dan Mares (Windows; supports MD5, SHA-1, SHA-2) and md5deep (cross-platform; supports MD5, SHA-1, SHA-256, Tiger, and Whirlpool).
A digression on hash collisions. Hash functions are sometimes misunderstood and some sources claim that no two files can have the same hash value. This is in theory, if not in fact, incorrect. Consider a hash function that provides a 128-bit hash value. There are, then, 2128 possible hash values. But there are an infinite number of possible files and ∞ >> 2128. Therefore, there have to be multiple files — in fact, there have to be an infinite number of files! — that have the same 128-bit hash value. (Now, while even this is theoretically correct, it is not true in practice because hash algorithms are designed to work with a limited message size, as mentioned above. For example, SHA-1, SHA-224, and SHA-256 produce hash values that are 160, 224, and 256 bits in length, respectively, and limit the message length to less than 264 bits; SHA-384 and all SHA-256 variants limit the message length to less than 2128 bits. Nevertheless, hopefully you get my point — and, alas, even if you don't, do know that there are multiple files that have the same MD5 or SHA-1 hash values.)
The difficulty is not necessarily in finding two files with the same hash, but in finding a second file that has the same hash value as a given first file. Consider this example. A human head has, generally, no more than ~150,000 hairs. Since there are more than 7 billion people on earth, we know that there are a lot of people with the same number of hairs on their head. Finding two people with the same number of hairs, then, would be relatively simple. The harder problem is choosing one person (say, you, the reader) and then finding another person who has the same number of hairs on their head as you have on yours.
This is somewhat similar to the Birthday Problem. We know from probability that if you choose a random group of ~23 people, the probability is about 50% that two will share a birthday (the probability goes up to 99.9% with a group of 70 people). However, if you randomly select one person in a group of 23 and try to find a match to that person, the probability is only about 6% of finding a match; you'd need a group of 253 for a 50% probability of a shared birthday to one of the people chosen at random (and a group of more than 4,000 to obtain a 99.9% probability).
What is hard to do, then, is to try to create a file that matches a given hash value so as to force a hash value collision — which is the reason that hash functions are used extensively for information security and computer forensics applications. Alas, researchers as far back as 2004 found that practical collision attacks could be launched on MD5, SHA-1, and other hash algorithms and, today, it is generally recognized that MD5 and SHA-1 are pretty much broken. Readers interested in this problem should read the following:
- AccessData. (2006, April). MD5 Collisions: The Effect on Computer Forensics. AccessData White Paper.
- Burr, W. (2006, March/April). Cryptographic hash standards: Where do we go from here? IEEE Security & Privacy, 4(2), 88-91.
- Dwyer, D. (2009, June 3). SHA-1 Collision Attacks Now 252. SecureWorks Research blog.
- Gutman, P., Naccache, D., & Palmer, C.C. (2005, May/June). When hashes collide. IEEE Security & Privacy, 3(3), 68-71.
- Kessler, G.C. (2016). The Impact of MD5 File Hash Collisions on Digital Forensic Imaging. Journal of Digital Forensics, Security & Law, 11(4), 129-138.
- Kessler, G.C. (2016). The Impact of SHA-1 File Hash Collisions on Digital Forensic Imaging: A Follow-Up Experiment. Journal of Digital Forensics, Security & Law, 11(4), 139-148.
- Klima, V. (2005, March). Finding MD5 Collisions - a Toy For a Notebook.
- Lee, R. (2009, January 7). Law Is Not A Science: Admissibility of Computer Evidence and MD5 Hashes. SANS Computer Forensics blog.
- Leurent, G. & Peyrin, T. (2020, January). SHA-1 is a Shambles: First Chosen-Prefix Collision on SHA-1 and Application to the PGP Web of Trust. Real World Crypto 2020.
- Leurent, G. & Peyrin, T. (2020, January). SHA-1 is a Shambles: First Chosen-Prefix Collision on SHA-1 and Application to the PGP Web of Trust. (paper)
- Stevens, M., Bursztein, E., Karpman, P., Albertini, A., & Markov, Y. (2017). The first collision for full SHA-1.
- Stevens, M., Karpman, P., & Peyrin, T. (2015, October 8). Freestart collision on full SHA-1. Cryptology ePrint Archive, Report 2015/967.
- Thompson, E. (2005, February). MD5 collisions and the impact on computer forensics. Digital Investigation, 2(1), 36-40.
- Wang, X., Feng, D., Lai, X., & Yu, H. (2004, August). Collisions for Hash Functions MD4, MD5, HAVAL-128 and RIPEMD.
- Wang, X., Yin, Y.L., & Yu, H. (2005, February 13). Collision Search Attacks on SHA1.
Readers are also referred to the Eindhoven University of Technology HashClash Project Web site. for For additional information on hash functions, see David Hopwood's MessageDigest Algorithms page and Peter Selinger's MD5 Collision Demo page. For historical purposes, take a look at the situation with hash collisions, circa 2005, in RFC 4270.
In October 2015, the SHA-1 Freestart Collision was announced; see a report by Bruce Schneier and the developers of the attack (as well as the paper above by Stevens et al. (2015)). In February 2017, the first SHA-1 collision was announced on the Google Security Blog and Centrum Wiskunde & Informatica's Shattered page. See also the paper by Stevens et al. (2017), listed above. If this isn't enough, see the SHA-1 is a Shambles Web page and the Leurent & Peyrin paper, listed above.
For an interesting twist on this discussion, read about the Nostradamus attack reported at Predicting the winner of the 2008 US Presidential Elections using a Sony PlayStation 3 (by M. Stevens, A.K. Lenstra, and B. de Weger, November 2007).
Finally, note that certain extensions of hash functions are used for a variety of information security and digital forensics applications, such as:
- Hash libraries, aka hashsets, are sets of hash values corresponding to known files. A hashset containing the hash values of all files known to be a part of a given operating system, for example, could form a set of known good files, and could be ignored in an investigation for malware or other suspicious file, whereas as hash library of known child pornographic images could form a set of known bad files and be the target of such an investigation.
- Rolling hashes refer to a set of hash values that are computed based upon a fixed-length "sliding window" through the input. As an example, a hash value might be computed on bytes 1-10 of a file, then on bytes 2-11, 3-12, 4-13, etc.
- Fuzzy hashes are an area of intense research and represent hash values that represent two inputs that are similar. Fuzzy hashes are used to detect documents, images, or other files that are close to each other with respect to content. See "Fuzzy Hashing" by Jesse Kornblum for a good treatment of this topic.
3.4. Why Three Encryption Techniques?
So, why are there so many different types of cryptographic schemes? Why can't we do everything we need with just one?
The answer is that each scheme is optimized for some specific cryptographic application(s). Hash functions, for example, are well-suited for ensuring data integrity because any change made to the contents of a message will result in the receiver calculating a different hash value than the one placed in the transmission by the sender. Since it is highly unlikely that two different messages will yield the same hash value, data integrity is ensured to a high degree of confidence.
Secret key cryptography, on the other hand, is ideally suited to encrypting messages, thus providing privacy and confidentiality. The sender can generate a session key on a per-message basis to encrypt the message; the receiver, of course, needs the same session key in order to decrypt the message.
Key exchange, of course, is a key application of public key cryptography (no pun intended). Asymmetric schemes can also be used for non-repudiation and user authentication; if the receiver can obtain the session key encrypted with the sender's private key, then only this sender could have sent the message. Public key cryptography could, theoretically, also be used to encrypt messages although this is rarely done because secret key cryptography algorithms can generally be executed up to 1000 times faster than public key cryptography algorithms.
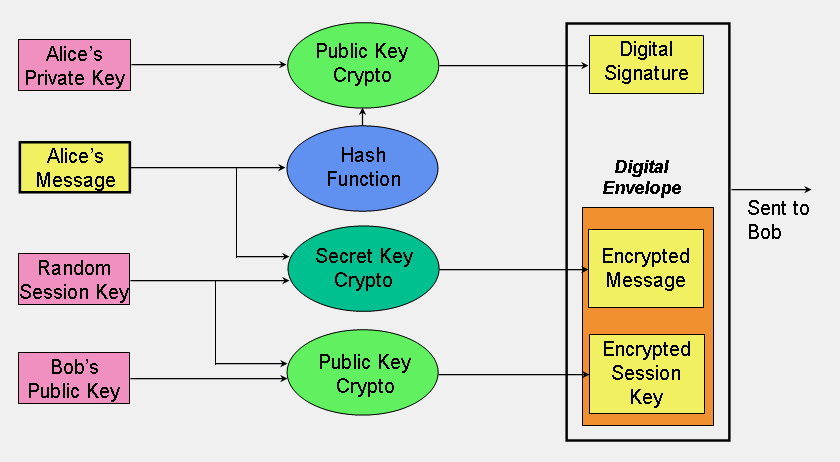
FIGURE 4: Use of the three cryptographic techniques for secure communication. |
Figure 4 puts all of this together and shows how a hybrid cryptographic scheme combines all of these functions to form a secure transmission comprising a digital signature and digital envelope. In this example, the sender of the message is Alice and the receiver is Bob.
A digital envelope comprises an encrypted message and an encrypted session key. Alice uses secret key cryptography to encrypt her message using the session key, which she generates at random with each session. Alice then encrypts the session key using Bob's public key. The encrypted message and encrypted session key together form the digital envelope. Upon receipt, Bob recovers the session secret key using his private key and then decrypts the encrypted message.
The digital signature is formed in two steps. First, Alice computes the hash value of her message; next, she encrypts the hash value with her private key. Upon receipt of the digital signature, Bob recovers the hash value calculated by Alice by decrypting the digital signature with Alice's public key. Bob can then apply the hash function to Alice's original message, which he has already decrypted (see previous paragraph). If the resultant hash value is not the same as the value supplied by Alice, then Bob knows that the message has been altered; if the hash values are the same, Bob should believe that the message he received is identical to the one that Alice sent.
This scheme also provides nonrepudiation since it proves that Alice sent the message; if the hash value recovered by Bob using Alice's public key proves that the message has not been altered, then only Alice could have created the digital signature. Bob also has proof that he is the intended receiver; if he can correctly decrypt the message, then he must have correctly decrypted the session key meaning that his is the correct private key.
This diagram purposely suggests a cryptosystem where the session key is used for just a single session. Even if this session key is somehow broken, only this session will be compromised; the session key for the next session is not based upon the key for this session, just as this session's key was not dependent on the key from the previous session. This is known as Perfect Forward Secrecy; you might lose one session key due to a compromise but you won't lose all of them. (This was an issue in the 2014 OpenSSL vulnerability known as Heartbleed.)
The system described here is one where we basically encrypt the secret session key with the receiver's public key. While this generic scheme works well, it causes some incompatibilities in practice. RFC 9180, released in early 2022, describes a new approach to building a Hybrid Public Key Encryption (HPKE) process. HPKE was designed specifically to be simple, reusable, and future-proof. A nice description of the process can be found in a blog posting titled, "HPKE: Standardizing Public-Key Encryption (Finally!)" (C. Wood).
3.5. The Significance of Key Length
In a 1998 article in the industry literature, a writer made the claim that 56-bit keys did not provide as adequate protection for DES at that time as they did in 1975 because computers were 1000 times faster in 1998 than in 1975. Therefore, the writer went on, we needed 56,000-bit keys in 1998 instead of 56-bit keys to provide adequate protection. The conclusion was then drawn that because 56,000-bit keys are infeasible (true), we should accept the fact that we have to live with weak cryptography (false!). The major error here is that the writer did not take into account that the number of possible key values double whenever a single bit is added to the key length; thus, a 57-bit key has twice as many values as a 56-bit key (because 257 is two times 256). In fact, a 66-bit key would have 1024 times more values than a 56-bit key.
But this does bring up the question — "What is the significance of key length as it affects the level of protection?"
In cryptography, size does matter. The larger the key, the harder it is to crack a block of encrypted data. The reason that large keys offer more protection is almost obvious; computers have made it easier to attack ciphertext by using brute force methods rather than by attacking the mathematics (which are generally well-known anyway). With a brute force attack, the attacker merely generates every possible key and applies it to the ciphertext. Any resulting plaintext that makes sense offers a candidate for a legitimate key. This was the basis, of course, of the EFF's attack on DES.
Until the mid-1990s or so, brute force attacks were beyond the capabilities of computers that were within the budget of the attacker community. By that time, however, significant compute power was typically available and accessible. General-purpose computers such as PCs were already being used for brute force attacks. For serious attackers with money to spend, such as some large companies or governments, Field Programmable Gate Array (FPGA) or Application-Specific Integrated Circuits (ASIC) technology offered the ability to build specialized chips that could provide even faster and cheaper solutions than a PC. As an example, the AT&T Optimized Reconfigurable Cell Array (ORCA) FPGA chip cost about $200 and could test 30 million DES keys per second, while a $10 ASIC chip could test 200 million DES keys per second; compare that to a PC which might be able to test 40,000 keys per second. Distributed attacks, harnessing the power of up to tens of thousands of powerful CPUs, are now commonly employed to try to brute-force crypto keys.
| Type of Attacker | Budget | Tool | Time and Cost Per Key Recovered |
Key Length Needed For Protection In Late-1995 | |
|---|---|---|---|---|---|
| 40 bits | 56 bits | ||||
| Pedestrian Hacker | Tiny | Scavenged computer time |
1 week | Infeasible | 45 |
| $400 | FPGA | 5 hours ($0.08) |
38 years ($5,000) |
50 | |
| Small Business | $10,000 | FPGA | 12 minutes ($0.08) |
18 months ($5,000) |
55 |
| Corporate Department | $300K | FPGA | 24 seconds ($0.08) |
19 days ($5,000) |
60 |
| ASIC | 0.18 seconds ($0.001) |
3 hours ($38) | |||
| Big Company | $10M | FPGA | 7 seconds ($0.08) |
13 hours ($5,000) |
70 |
| ASIC | 0.005 seconds ($0.001) |
6 minutes ($38) | |||
| Intelligence Agency | $300M | ASIC | 0.0002 seconds ($0.001) |
12 seconds ($38) |
75 |
Table 2 — from a 1996 article discussing both why exporting 40-bit keys was, in essence, no crypto at all and why DES' days were numbered — shows what DES key sizes were needed to protect data from attackers with different time and financial resources. This information was not merely academic; one of the basic tenets of any security system is to have an idea of what you are protecting and from whom are you protecting it! The table clearly shows that a 40-bit key was essentially worthless against even the most unsophisticated attacker. On the other hand, 56-bit keys were fairly strong unless you might be subject to some pretty serious corporate or government espionage. But note that even 56-bit keys were clearly on the decline in their value and that the times in the table were worst cases.
So, how big is big enough? DES, invented in 1975, was still in use at the turn of the century, nearly 25 years later. If we take that to be a design criteria (i.e., a 20-plus year lifetime) and we believe Moore's Law ("computing power doubles every 18 months"), then a key size extension of 14 bits (i.e., a factor of more than 16,000) should be adequate. The 1975 DES proposal suggested 56-bit keys; by 1995, a 70-bit key would have been required to offer equal protection and an 85-bit key necessary by 2015.
A 256- or 512-bit SKC key will probably suffice for some time because that length keeps us ahead of the brute force capabilities of the attackers. Note that while a large key is good, a huge key may not always be better; for example, expanding PKC keys beyond the current 2048- or 4096-bit lengths doesn't add any necessary protection at this time. Weaknesses in cryptosystems are largely based upon key management rather than weak keys.
Much of the discussion above, including the table, is based on the paper "Minimal Key Lengths for Symmetric Ciphers to Provide Adequate Commercial Security" by M. Blaze, W. Diffie, R.L. Rivest, B. Schneier, T. Shimomura, E. Thompson, and M. Wiener (1996).
The most effective large-number factoring methods today use a mathematical Number Field Sieve to find a certain number of relationships and then uses a matrix operation to solve a linear equation to produce the two prime factors. The sieve step actually involves a large number of operations that can be performed in parallel; solving the linear equation, however, requires a supercomputer. Indeed, finding the solution to the RSA-140 challenge in February 1999 — factoring a 140-digit (465-bit) prime number — required 200 computers across the Internet about 4 weeks for the first step and a Cray computer 100 hours and 810 MB of memory to do the second step.
In early 1999, Shamir (of RSA fame) described a new machine that could increase factorization speed by 2-3 orders of magnitude. Although no detailed plans were provided nor is one known to have been built, the concepts of TWINKLE (The Weizmann Institute Key Locating Engine) could result in a specialized piece of hardware that would cost about $5000 and have the processing power of 100-1000 PCs. There still appear to be many engineering details that have to be worked out before such a machine could be built. Furthermore, the hardware improves the sieve step only; the matrix operation is not optimized at all by this design and the complexity of this step grows rapidly with key length, both in terms of processing time and memory requirements. Nevertheless, this plan conceptually puts 512-bit keys within reach of being factored. Although most PKC schemes allow keys that are 1024 bits and longer, Shamir claims that 512-bit RSA keys "protect 95% of today's E-commerce on the Internet." (See Bruce Schneier's Crypto-Gram (May 15, 1999) for more information.)
It is also interesting to note that while cryptography is good and strong cryptography is better, long keys may disrupt the nature of the randomness of data files. Shamir and van Someren ("Playing hide and seek with stored keys") have noted that a new generation of viruses can be written that will find files encrypted with long keys, making them easier to find by intruders and, therefore, more prone to attack.
Finally, U.S. government policy has tightly controlled the export of crypto products since World War II. Until the mid-1990s, export outside of North America of cryptographic products using keys greater than 40 bits in length was prohibited, which made those products essentially worthless in the marketplace, particularly for electronic commerce; today, crypto products are widely available on the Internet without restriction.
Without meaning to editorialize too much in this tutorial, a bit of historical context might be helpful. In the mid-1990s, the U.S. Department of Commerce still classified cryptography as a munition and limited the export of any products that contained crypto. For that reason, browsers in the 1995 era, such as Internet Explorer and Netscape, had a domestic version with 128-bit encryption (downloadable only in the U.S.) and an export version with 40-bit encryption. Many cryptographers felt that the export limitations should be lifted because they only applied to U.S. products and seemed to have been put into place by policy makers who believed that only the U.S. knew how to build strong crypto algorithms, ignoring the work ongoing in Australia, Canada, Israel, South Africa, the U.K., and other locations in the 1990s. Those restrictions were lifted by 1996 or 1997, but there is still a prevailing attitude, apparently, that U.S. crypto algorithms are the only strong ones around; consider Bruce Schneier's blog in June 2016 titled "CIA Director John Brennan Pretends Foreign Cryptography Doesn't Exist." Cryptography is a decidedly international game today; note the many countries mentioned above as having developed various algorithms, not the least of which is the fact that NIST's Advanced Encryption Standard employs an algorithm submitted by cryptographers from Belgium. For more evidence, see Schneier's Worldwide Encryption Products Survey (February 2016).
On a related topic, public key crypto schemes can be used for several purposes, including key exchange, digital signatures, authentication, and more. In those PKC systems used for SKC key exchange, the PKC key lengths are chosen so as to be resistant to some selected level of attack. The length of the secret keys exchanged via that system have to have at least the same level of attack resistance. Thus, the three parameters of such a system — system strength, secret key strength, and public key strength — must be matched. This topic is explored in more detail in Determining Strengths For Public Keys Used For Exchanging Symmetric Keys (RFC 3766).
4. TRUST MODELS
Secure use of cryptography requires trust. While secret key cryptography can ensure message confidentiality and hash codes can ensure integrity, none of this works without trust. In SKC, Alice and Bob had to share a secret key. PKC solved the secret distribution problem, but how does Alice really know that Bob is who he says he is? Just because Bob has a public and private key, and purports to be "Bob," how does Alice know that a malicious person (Mallory) is not pretending to be Bob?
There are a number of trust models employed by various cryptographic schemes. This section will explore three of them:
- The web of trust employed by Pretty Good Privacy (PGP) users, who hold their own set of trusted public keys.
- Kerberos, a secret key distribution scheme using a trusted third party.
- Certificates, which allow a set of trusted third parties to authenticate each other and, by implication, each other's users.
Each of these trust models differs in complexity, general applicability, scope, and scalability.
4.1. PGP Web of Trust
Pretty Good Privacy (described more below in Section 5.5) is a widely used private e-mail scheme based on public key methods. A PGP user maintains a local keyring of all their known and trusted public keys. The user makes their own determination about the trustworthiness of a key using what is called a "web of trust."
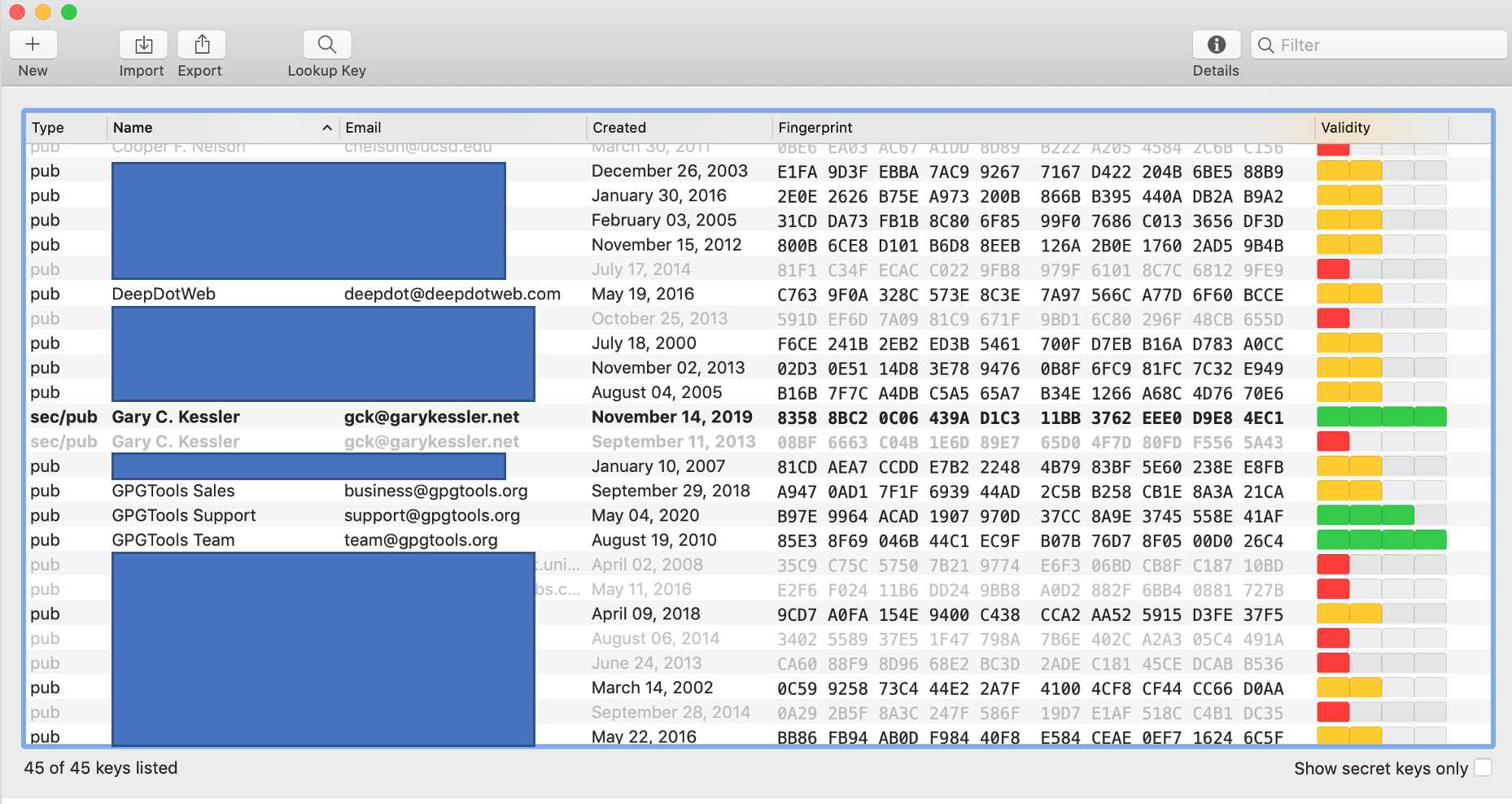
FIGURE 5: GPG keychain. |
Figure 5 shows a PGP-formatted keychain from the GNU Privacy Guard (GPG) software, an implementation of the OpenPGP standard. This is a section of my keychain, so only includes public keys from individuals whom I know and, presumably, trust. Note that keys are associated with e-mail addresses rather than individual names.
In general, the PGP Web of trust works as follows. Suppose that Alice needs Bob's public key. Alice could just ask Bob for it directly via e-mail or download the public key from a PGP key server; this server might a well-known PGP key repository or a site that Bob maintains himself. In fact, Bob's public key might be stored or listed in many places. (My public key, for example, can be found at https://www.garykessler.net/pubkey.html or at several public PGP key servers, including https://keys.openpgp.org.) Alice is prepared to believe that Bob's public key, as stored at these locations, is valid.
Suppose Carol claims to hold Bob's public key and offers to give the key to Alice. How does Alice know that Carol's version of Bob's key is valid or if Carol is actually giving Alice a key that will allow Mallory access to messages? The answer is, "It depends." If Alice trusts Carol and Carol says that she thinks that her version of Bob's key is valid, then Alice may — at her option — trust that key. And trust is not necessarily transitive; if Dave has a copy of Bob's key and Carol trusts Dave, it does not necessarily follow that Alice trusts Dave even if she does trust Carol.
The point here is that who Alice trusts and how she makes that determination is strictly up to Alice. PGP makes no statement and has no protocol about how one user determines whether they trust another user or not. In any case, encryption and signatures based on public keys can only be used when the appropriate public key is on the user's keyring.
4.2. Kerberos
Kerberos is a commonly used authentication scheme on the Internet. Developed by MIT's Project Athena, Kerberos is named for the three-headed dog who, according to Greek mythology, guards the entrance of Hades (rather than the exit, for some reason!).
Kerberos employs a client/server architecture and provides user-to-server authentication rather than host-to-host authentication. In this model, security and authentication will be based on secret key technology where every host on the network has its own secret key. It would clearly be unmanageable if every host had to know the keys of all other hosts so a secure, trusted host somewhere on the network, known as a Key Distribution Center (KDC), knows the keys for all of the hosts (or at least some of the hosts within a portion of the network, called a realm). In this way, when a new node is brought online, only the KDC and the new node need to be configured with the node's key; keys can be distributed physically or by some other secure means.
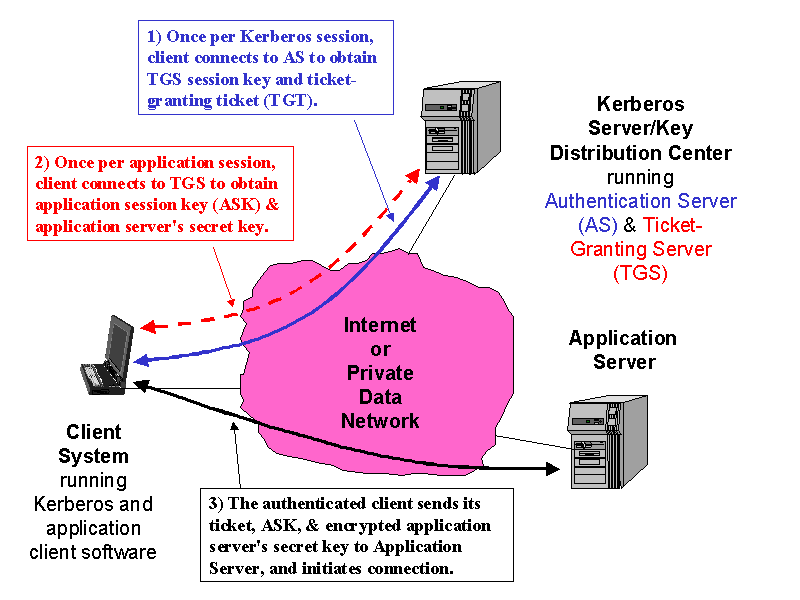
FIGURE 6: Kerberos architecture. |
The Kerberos Server/KDC has two main functions (Figure 6), known as the Authentication Server (AS) and Ticket-Granting Server (TGS). The steps in establishing an authenticated session between an application client and the application server are:
- The Kerberos client software establishes a connection with the Kerberos server's AS function. The AS first authenticates that the client is who it purports to be. The AS then provides the client with a secret key for this login session (the TGS session key) and a ticket-granting ticket (TGT), which gives the client permission to talk to the TGS. The ticket has a finite lifetime so that the authentication process is repeated periodically.
- The client now communicates with the TGS to obtain the Application Server's key so that it (the client) can establish a connection to the service it wants. The client supplies the TGS with the TGS session key and TGT; the TGS responds with an application session key (ASK) and an encrypted form of the Application Server's secret key; this secret key is never sent on the network in any other form.
- The client has now authenticated itself and can prove its identity to the Application Server by supplying the Kerberos ticket, application session key, and encrypted Application Server secret key. The Application Server responds with similarly encrypted information to authenticate itself to the client. At this point, the client can initiate the intended service requests (e.g., Telnet, FTP, HTTP, or e-commerce transaction session establishment).
The current version of this protocol is Kerberos V5 (described in RFC 1510). While the details of their operation, functional capabilities, and message formats are different, the conceptual overview above pretty much holds for both. One primary difference is that Kerberos V4 uses only DES to generate keys and encrypt messages, while V5 allows other schemes to be employed (although DES is still the most widely algorithm used).
4.3. Public Key Certificates and Certificate Authorities
Certificates and Certificate Authorities (CA) are necessary for widespread use of cryptography for e-commerce applications. While a combination of secret and public key cryptography can solve the business issues discussed above, crypto cannot alone address the trust issues that must exist between a customer and vendor in the very fluid, very dynamic e-commerce relationship. How, for example, does one site obtain another party's public key? How does a recipient determine if a public key really belongs to the sender? How does the recipient know that the sender is using their public key for a legitimate purpose for which they are authorized? When does a public key expire? How can a key be revoked in case of compromise or loss?
The basic concept of a certificate is one that is familiar to all of us. A driver's license, credit card, or SCUBA certification, for example, identify us to others, indicate something that we are authorized to do, have an expiration date, and identify the authority that granted the certificate.
As complicated as this may sound, it really isn't. Consider driver's licenses. I have one issued by the State of Florida. The license establishes my identity, indicates the type of vehicles that I can operate and the fact that I must wear corrective lenses while doing so, identifies the issuing authority, and notes that I am an organ donor. When I drive in other states, the other jurisdictions throughout the U.S. recognize the authority of Florida to issue this "certificate" and they trust the information it contains. When I leave the U.S., everything changes. When I am in Aruba, Australia, Canada, Israel, and many other countries, they will accept not the Florida license, per se, but any license issued in the U.S. This analogy represents the certificate trust chain, where even certificates carry certificates.
For purposes of electronic transactions, certificates are digital documents. The specific functions of the certificate include:
- Establish identity: Associate, or bind, a public key to an individual, organization, corporate position, or other entity.
- Assign authority: Establish what actions the holder may or may not take based upon this certificate.
- Secure confidential information (e.g., encrypting the session's symmetric key for data confidentiality).
Typically, a certificate contains a public key, a name, an expiration date, the name of the authority that issued the certificate (and, therefore, is vouching for the identity of the user), a serial number, any pertinent policies describing how the certificate was issued and/or how the certificate may be used, the digital signature of the certificate issuer, and perhaps other information.

FIGURE 7: VeriSign Class 3 certificate. |
A sample abbreviated certificate is shown in Figure 7. This is a typical certificate found in a browser, in this case, Mozilla Firefox (MacOS). While this is a certificate issued by VeriSign, many root-level certificates can be found shipped with browsers. When the browser makes a connection to a secure Web site, the Web server sends its public key certificate to the browser. The browser then checks the certificate's signature against the public key that it has stored; if there is a match, the certificate is taken as valid and the Web site verified by this certificate is considered to be "trusted."
The most widely accepted certificate format is the one defined in International Telecommunication Union Telecommunication Standardization Sector (ITU-T) Recommendation X.509. Rec. X.509 is a specification used around the world and any applications complying with X.509 can share certificates. Most certificates today comply with X.509 Version 3 and contain the following information:
- Version number
- Certificate serial number
- Signature algorithm identifier
- Issuer's name and unique identifier
- Validity (or operational) period
- Subject's name and unique identifier
- Subject public key information
- Standard extensions
- Certificate appropriate use definition
- Key usage limitation definition
- Certificate policy information
- Other extensions
- Application-specific
- CA-specific
Certificate authorities are the repositories for public keys and can be any agency that issues certificates. A company, for example, may issue certificates to its employees, a college/university to its students, a store to its customers, an Internet service provider to its users, or a government to its constituents.
When a sender needs an intended receiver's public key, the sender must get that key from the receiver's CA. That scheme is straight-forward if the sender and receiver have certificates issued by the same CA. If not, how does the sender know to trust the foreign CA? One industry wag has noted, about trust: "You are either born with it or have it granted upon you." Thus, some CAs will be trusted because they are known to be reputable, such as the CAs operated by AT&T Services, Comodo, DigiCert (formerly GTE Cybertrust), EnTrust, Broadcom (formerly Symantec, formerly VeriSign), and Thawte. CAs, in turn, form trust relationships with other CAs. Thus, if a user queries a foreign CA for information, the user may ask to see a list of CAs that establish a "chain of trust" back to the user.
One major feature to look for in a CA is their identification policies and procedures. When a user generates a key pair and forwards the public key to a CA, the CA has to check the sender's identification and takes any steps necessary to assure itself that the request is really coming from the advertised sender. Different CAs have different identification policies and will, therefore, be trusted differently by other CAs. Verification of identity is just one of many issues that are part of a CA's Certification Practice Statement (CPS) and policies; other issues include how the CA protects the public keys in its care, how lost or compromised keys are revoked, and how the CA protects its own private keys.
As a final note, CAs are not immune to attack and certificates themselves are able to be counterfeited. One of the first such episodes occurred at the turn of the century; on January 29 and 30, 2001, two VeriSign Class 3 code-signing digital certificates were issued to an individual who fraudulently claimed to be a Microsoft employee (CERT/CC CA-2001-04 and Microsoft Security Bulletin MS01-017 - Critical). Problems have continued over the years; good write-ups on this can be found at "Another Certification Authority Breached (the 12th!)" and "How Cybercrime Exploits Digital Certificates." Readers are also urged to read "Certification Authorities Under Attack: A Plea for Certificate Legitimation" (Oppliger, R., January/February 2014, IEEE Internet Computing, 18(1), 40-47).
As a partial way to address this issue, the Internet Security Research Group (ISRG) designed the Automated Certificate Management Environment (ACME) protocol. ACME is a communications protocol that streamlines the process of deploying a Public Key Infrastructure (PKI) by automating interactions between CAs and Web servers that wish to obtain a certificate. More information can be found at the Let's Encrypt Web site, an ACME-based CA service provided by the ISRG.
4.4. Summary
The paragraphs above describe three very different trust models. It is hard to say that any one is better than the others; it depends upon your application. One of the biggest and fastest growing applications of cryptography today, though, is electronic commerce (e-commerce), a term that itself begs for a formal definition.
PGP's web of trust is easy to maintain and very much based on the reality of users as people. The model, however, is limited; just how many public keys can a single user reliably store and maintain? And what if you are using the "wrong" computer when you want to send a message and can't access your keyring? How easy it is to revoke a key if it is compromised? PGP may also not scale well to an e-commerce scenario of secure communication between total strangers on short-notice.
Kerberos overcomes many of the problems of PGP's web of trust, in that it is scalable and its scope can be very large. However, it also requires that the Kerberos server have a priori knowledge of all client systems prior to any transactions, which makes it unfeasible for "hit-and-run" client/server relationships as seen in e-commerce.
Certificates and the collection of CAs will form a PKI. In the early days of the Internet, every host had to maintain a list of every other host; the Domain Name System (DNS) introduced the idea of a distributed database for this purpose and the DNS is one of the key reasons that the Internet has grown as it has. A PKI will fill a similar void in the e-commerce and PKC realm.
While certificates and the benefits of a PKI are most often associated with electronic commerce, the applications for PKI are much broader and include secure electronic mail, payments and electronic checks, Electronic Data Interchange (EDI), secure transfer of Domain Name System (DNS) and routing information, electronic forms, and digitally signed documents. A single "global PKI" is still many years away, that is the ultimate goal of today's work as international electronic commerce changes the way in which we do business in a similar way in which the Internet has changed the way in which we communicate.
5. CRYPTOGRAPHIC ALGORITHMS IN ACTION
The paragraphs above have provided an overview of the different types of cryptographic algorithms, as well as some examples of some available protocols and schemes. Table 3 provides a list of some other noteworthy schemes and cryptosystems employed — or proposed — for a variety of functions, most notably electronic commerce and secure communication. The paragraphs below will show several real cryptographic applications that many of us employ (knowingly or not) everyday for password protection and private communication. Some of the schemes described below never were widely deployed but are still historically interesting, thus remain included here. This list is, by no means, exhaustive but describes items that are of significant current and/or historic importance (a subjective judgement, to be sure).
| Bitmessage | A decentralized, encrypted, peer-to-peer, trustless communications protocol for message exchange. The decentralized design, outlined in "Bitmessage: A Peer-to-Peer Message Authentication and Delivery System" (Warren, 2012), is conceptually based on the Bitcoin model. |
| Capstone | A now-defunct U.S. National Institute of Standards and Technology (NIST) and National Security Agency (NSA) project under the Bush Sr. and Clinton administrations for publicly available strong cryptography with keys escrowed by the government (NIST and the Treasury Dept.). Capstone included one or more tamper-proof computer chips for implementation (Clipper), a secret key encryption algorithm (Skipjack), digital signature algorithm (DSA), key exchange algorithm (KEA), and hash algorithm (SHA). |
| Challenge-Handshake Authentication Protocol (CHAP) | An authentication scheme that allows one party to prove who they are to a second party by demonstrating knowledge of a shared secret without actually divulging that shared secret to a third party who might be listening. Described in RFC 1994. |
| Chips-Message Robust Authentication (CHIMERA) | A scheme proposed for authenticating navigation data and the spreading code of civilian signals in the Global Positioning System (GPS). This is an anti-spoofing mechanism to protect the unencrypted civilian signals; GPS military signals are encrypted. |
| Clipper | The computer chip that would implement the Skipjack encryption scheme. The Clipper chip was to have had a deliberate backdoor so that material encrypted with this device would not be beyond the government's reach. Described in 1993, Clipper was dead by 1996. See also EPIC's The Clipper Chip Web page. |
| Cryptography Research and Evaluation Committees (CRYPTEC) | Similar in concept to the NIST AES process and NESSIE, CRYPTEC is the Japanese government's process to evaluate algorithms submitted for government and industry applications. CRYPTEX maintains a list of public key and secret key ciphers, hash functions, MACs, and other crypto algorithms approved for various applications in government environments. |
| Derived Unique Key Per Transaction (DUKPT) | A key management scheme used for debit and credit card verification with point-of-sale (POS) transaction systems, automated teller machines (ATMs), and other financial applications. In DUKPT, a unique key is derived for each transaction based upon a fixed, shared key in such a way that knowledge of one derived key does not easily yield knowledge of other keys (including the fixed key). Therefore, if one of the derived keys is compromised, neither past nor subsequent transactions are endangered. DUKPT is specified in American National Standard (ANS) ANSI X9.24-1:2009 (Retail Financial Services Symmetric Key Management Part 1: Using Symmetric Techniques) and can be purchased at the ANSI X9.24 Web page. |
| ECRYPT Stream Cipher Project (eSTREAM) | The eSTREAM project came about as a result of the failure of the NESSIE project to produce a stream cipher that survived cryptanalysis. eSTREAM ran from 2004 to 2008 with the primary purpose of promoting the design of efficient and compact stream ciphers. As of September 2008, the eSTREAM suite contains seven ciphers. |
| Escrowed Encryption Standard (EES) | Largely unused, a controversial crypto scheme employing the SKIPJACK secret key crypto algorithm and a Law Enforcement Access Field (LEAF) creation method. LEAF was one part of the key escrow system and allowed for decryption of ciphertext messages that had been intercepted by law enforcement agencies. Described more in FIPS PUB 185 (archived; no longer in force). |
| Federal Information Processing Standards (FIPS) | These computer security- and crypto-related FIPS PUBs are produced by the U.S. National Institute of Standards and Technology (NIST) as standards for the U.S. Government. Current Federal Information Processing Standards (FIPS) related to cryptography include:
|
| Fortezza | A PCMCIA card developed by NSA that implements the Capstone algorithms, intended for use with the Defense Messaging Service (DMS). Originally called Tessera. |
| GOST | GOST is a family of algorithms defined in the Russian cryptographic standards. Although most of the specifications are written in Russian, a series of RFCs describe some of the aspects so that the algorithms can be used effectively in Internet applications:
|
| IP Security (IPsec) | The IPsec protocol suite is used to provide privacy and authentication services at the IP layer. An overview of the protocol suite and of the documents comprising IPsec can be found in RFC 2411. Other documents include:
In addition, RFC 6379 describes Suite B Cryptographic Suites for IPsec and RFC 6380 describes the Suite B profile for IPsec. IPsec was first proposed for use with IP version 6 (IPv6), but can also be employed with the current IP version, IPv4. (See more detail about IPsec below in Section 5.6.) |
| Internet Security Association and Key Management Protocol (ISAKMP/OAKLEY) | ISAKMP/OAKLEY provide an infrastructure for Internet secure communications. ISAKMP, designed by the National Security Agency (NSA) and described in RFC 2408, is a framework for key management and security associations, independent of the key generation and cryptographic algorithms actually employed. The OAKLEY Key Determination Protocol, described in RFC 2412, is a key determination and distribution protocol using a variation of Diffie-Hellman. |
| Kerberos | A secret key encryption and authentication system, designed to authenticate requests for network resources within a user domain rather than to authenticate messages. Kerberos also uses a trusted third-party approach; a client communications with the Kerberos server to obtain "credentials" so that it may access services at the application server. Kerberos V4 used DES to generate keys and encrypt messages; Kerberos V5 uses DES and other schemes for key generation.
Microsoft added support for Kerberos V5 — with some proprietary extensions — in Windows 2000 Active Directory. There are many Kerberos articles posted at Microsoft's Knowledge Base, notably "Kerberos Explained." |
| Keyed-Hash Message Authentication Code (HMAC) | A message authentication scheme based upon secret key cryptography and the secret key shared between two parties rather than public key methods. Described in FIPS PUB 198 and RFC 2104. (See Section 5.19 below for details on HMAC operation.) |
| Message Digest Cipher (MDC) | Invented by Peter Gutman, MDC turns a one-way hash function into a block cipher. |
| MIME Object Security Services (MOSS) | Designed as a successor to PEM to provide PEM-based security services to MIME messages. Described in RFC 1848. Never widely implemented and now defunct. |
| Mujahedeen Secrets | A Windows GUI, PGP-like cryptosystem. Developed by supporters of Al-Qaeda, the program employs the five finalist AES algorithms, namely, MARS, RC6, Rijndael, Serpent, and Twofish. Also described in Inspire Magazine, Issue 1, pp. 41-44 and Inspire Magazine, Issue 2, pp. 58-59. Additional related information can also be found in "How Al-Qaeda Uses Encryption Post-Snowden (Part 2)." |
| New European Schemes for Signatures, Integrity and Encryption (NESSIE) | NESSIE was an independent project meant to augment the work of NIST during the AES adoption process by putting out an open call for new cryptographic primitives. The NESSIE project ran from about 2000-2003. While several new block cipher, PKC, MAC, and digital signature algorithms were found during the NESSIE process, no new stream cipher survived cryptanalysis. As a result, the ECRYPT Stream Cipher Project (eSTREAM) was created. |
| NSA Suite B Cryptography | An NSA standard for securing information at the SECRET level. Defines use of:
RFC 6239 describes Suite B Cryptographic Suites for Secure Shell (SSH) and RFC 6379 describes Suite B Cryptographic Suites for Secure IP (IPsec). RFC 8423 reclassifies the RFCs related to the Suite B cryptographic algorithms as Historic, and it discusses the reasons for doing so. |
| The OPAQUE Augmented Password-Authenticated Key Exchange (aPAKE) Protocol | Augmented (or Asymmetric) Password Authenticated Key Exchange (aPAKE) protocols are designed to provide password authentication and mutually authenticated key exchange in a client-server setting without relying on PKI (except during client registration) and without disclosing passwords to servers or other entities other than the client machine. A secure aPAKE should provide the best possible security for a password protocol. Indeed, some attacks are inevitable, such as online impersonation attempts with guessed client passwords and offline dictionary attacks upon the compromise of a server and leakage of its credential file. In the latter case, the attacker learns a mapping of a client's password under a one-way function and uses such a mapping to validate potential guesses for the password. It is crucially important for the password protocol to use an unpredictable one-way mapping. Otherwise, the attacker can pre-compute a deterministic list of mapped passwords leading to almost instantaneous leakage of passwords upon server compromise. RFC 9807 describes OPAQUE, an aPAKE protocol that is secure against pre-computation attacks. OPAQUE provides forward secrecy with respect to password leakage while also hiding the password from the server, even during password registration. OPAQUE allows applications to increase the difficulty of offline dictionary attacks via iterated hashing or other key-stretching schemes. OPAQUE is also extensible, allowing clients to safely store and retrieve arbitrary application data on servers using only their password. (This summary is from RFC 9807.) |
| Pretty Good Privacy (PGP) | A family of cryptographic routines for e-mail, file, and disk encryption developed by Philip Zimmermann. PGP 2.6.x uses RSA for key management and digital signatures, IDEA for message encryption, and MD5 for computing the message's hash value; more information can also be found in RFC 1991. PGP 5.x (formerly known as "PGP 3") uses Diffie-Hellman/DSS for key management and digital signatures; IDEA, CAST, or 3DES for message encryption; and MD5 or SHA for computing the message's hash value. OpenPGP, described in RFC 9580, is an open definition of security software based on PGP 5.x. The GNU Privacy Guard (GPG) is a free software version of OpenPGP.
(See more detail about PGP below in Section 5.5.) |
| Privacy Enhanced Mail (PEM) | An IETF standard for secure electronic mail over the Internet, including provisions for encryption (DES), authentication, and key management (DES, RSA). Developed by the IETF but never widely used. Described in the following RFCs: |
| Private Communication Technology (PCT) | Developed by Microsoft for secure communication on the Internet. PCT supported Diffie-Hellman, Fortezza, and RSA for key establishment; DES, RC2, RC4, and triple-DES for encryption; and DSA and RSA message signatures. Never widely used; superseded by SSL and TLS. |
| Secure Electronic Transaction (SET) | A communications protocol for securing credit card transactions, developed by MasterCard and VISA, in cooperation with IBM, Microsoft, RSA, and other companies. Merged two other protocols: Secure Electronic Payment Protocol (SEPP), an open specification for secure bank card transactions over the Internet developed by CyberCash, GTE, IBM, MasterCard, and Netscape; and Secure Transaction Technology (STT), a secure payment protocol developed by Microsoft and Visa International. Supports DES and RC4 for encryption, and RSA for signatures, key exchange, and public key encryption of bank card numbers. SET V1.0 is described in Book 1, Book 2, and Book 3. SET has been superseded by SSL and TLS. |
| Secure Hypertext Transfer Protocol (S-HTTP) | An extension to HTTP to provide secure exchange of documents over the World Wide Web. Supported algorithms include RSA and Kerberos for key exchange, DES, IDEA, RC2, and Triple-DES for encryption. Described in RFC 2660. S-HTTP was never as widely used as HTTP over SSL (https). |
| Secure Multipurpose Internet Mail Extensions (S/MIME) | An IETF secure e-mail scheme superseding PEM, and adding digital signature and encryption capability to Internet MIME messages. S/MIME Version 3.1 is described in RFCs 3850 and 3851, and employs the Cryptographic Message Syntax described in RFCs 3369 and 3370.
(More detail about S/MIME can be found below in Section 5.15.) |
| Secure Sockets Layer (SSL) | Developed in 1995 by Netscape Communications to provide application-independent security and privacy over the Internet. SSL is designed so that protocols such as HTTP, FTP (File Transfer Protocol), and Telnet can operate over it transparently. SSL allows both server authentication (mandatory) and client authentication (optional). RSA is used during negotiation to exchange keys and identify the actual cryptographic algorithm (DES, IDEA, RC2, RC4, or 3DES) to use for the session. SSL also uses MD5 for message digests and X.509 public key certificates. SSL was found to be breakable soon after the IETF announced formation of group to work on TLS and RFC 6176 specifically prohibits the use of SSL v2.0 by TLS clients. SSL version 3.0 is described in RFC 6101. All versions of SSL are now deprecated in favor of TLS; TLS v1.0 is sometimes referred to as "SSL v3.1."
(More detail about SSL can be found below in Section 5.7.) |
| Server Gated Cryptography (SGC) | Microsoft extension to SSL that provided strong encryption for online banking and other financial applications using RC2 (128-bit key), RC4 (128-bit key), DES (56-bit key), or 3DES (equivalent of 168-bit key). Use of SGC required a Windows NT Server running Internet Information Server (IIS) 4.0 with a valid SGC certificate. SGC was available in 32-bit Windows versions of Internet Explorer (IE) 4.0; support for Mac, Unix, and 16-bit Windows versions of IE was planned, but never materialized, and SGC was made moot when browsers started to ship with 128-bit encryption. |
| ShangMi (SM) Cipher Suites | A suite of authentication, encryption, and hash algorithms from the People's Republic of China.
|
| Signal Protocol | A protocol for providing end-to-end encryption for voice calls, video calls, and instant messaging (including group chats). Employing a combination of AES, ECC, and HMAC algorithms, it offers such features as confidentiality, integrity, authentication, forward/future secrecy, and message repudiation. Signal is particularly interesting because of its lineage and widespread use. The Signal Protocol's earliest versions were known as TextSecure, first developed by Open Whisper Systems in 2013. TextSecure itself was based on a 2004 protocol called Off-the-Record (OTR) Messaging, designed as an improvement over OpenPGP and S/MIME. TextSecure v2 (2014) introduced a scheme called the Axolotl Ratchet for key exchange and added additional communication features. After subsequent iterations improving key management (and the renaming of the key exchange protocol to Double Ratchet), additional cryptographic primitives, and the addition of an encrypted voice calling application (RedPhone), TextSecure was renamed Signal Protocol in 2016. The Ratchet key exchange algorithm is at the heart of the power of this system. Most messaging apps employ the users' public and private keys; the weakness here is that if the phone falls into someone else's hands, all of the messages on the device — including deleted messages — can be decrypted. The Ratchet algorithm generates a set of so-called "temporary keys" for each user, based upon that user's public/private key pair. When two users exchange messages, the Signal protocol creates a secret key by combining the temporary and permanent pairs of public and private keys for both users. Each message is assigned its own secret key. Because the generation of the secret key requires access to both users' private keys, it exists only on their two devices. The Signal Protocol is/has been employed in:
|
| Simple Authentication and Security Layer (SASL) | A framework for providing authentication and data security services in connection-oriented protocols (a la TCP), described in RFC 4422. It provides a structured interface and allows new protocols to reuse existing authentication mechanisms and allows old protocols to make use of new mechanisms.
It has been common practice on the Internet to permit anonymous access to various services, employing a plain-text password using a user name of "anonymous" and a password of an email address or some other identifying information. New IETF protocols disallow plain-text logins. The Anonymous SASL Mechanism (RFC 4505) provides a method for anonymous logins within the SASL framework. |
| Simple Key-Management for Internet Protocol (SKIP) | Key management scheme for secure IP communication, specifically for IPsec, and designed by Aziz and Diffie. SKIP essentially defines a public key infrastructure for the Internet and even uses X.509 certificates. Most public key cryptosystems assign keys on a per-session basis, which is inconvenient for the Internet since IP is connectionless. Instead, SKIP provides a basis for secure communication between any pair of Internet hosts. SKIP can employ DES, 3DES, IDEA, RC2, RC5, MD5, and SHA-1. As it happened, SKIP was not adopted for IPsec; IKE was selected instead. |
| SM9 | Chinese Standard GM/T0044-2016 SM9 (2016) is the Chinese national standard for Identity Based Cryptography. SM9 comprises three cryptographic algorithms, namely the Identity Based Digital Signature Algorithm, Identity Based Key Agreement Algorithm, and Identity Based Key Encapsulation Algorithm (allowing one party to securely send a symmetric key to another party). The SM9 scheme is also described in The SM9 Cryptographic Schemes (Z. Cheng). |
| Telegram | Telegram, launched in 2013, is a cloud-based instant messaging and voice over IP (VoIP) service, with client app software available for all major computer and mobile device operating systems. Telegram allows users to exchange messages, photos, videos, etc., and supplies end-to-end encryption using a protocol called MTProto. stickers, audio and files of any type. MTProto employs 256-bit AES, 2048-bit RSA, and Diffie-Hellman key exchange. There have been several controversies with Telegram, not the least of which has to do with the nationality of the founders and the true location of the business, as well as some operation issues. From a cryptological viewpoint, however, one cautionary tale can be found in "On the CCA (in)security of MTProto" (Jakobsen & Orlandi, 2015), who describe some of the crypto weaknesses of the protocol; specifically, that "MTProto does not satisfy the definitions of authenticated encryption (AE) or indistinguishability under chosen-ciphertext attack (IND-CCA)" (p. 1). |
| Transmission Control Protocol (TCP) encryption (tcpcrypt) | As of 2019, the majority of Internet TCP traffic is not encrypted. The two primary reasons for this are (1) many legacy protocols have no mechanism with which to employ encryption (e.g., without a command such as STARTSSL, the protocol cannot invoke use of any encryption) and (2) many legacy applications cannot be upgraded, so no new encryption can be added. The response from the IETF's TCP Increased Security Working Group was to define a transparent way within the transport layer (i.e., TCP) with which to invoke encryption. The TCP Encryption Negotiation Option (TCP-ENO) addresses these two problems with an out-of-band, fully backward-compatible TCP option with which to negotiate use of encryption. TCP-ENO is described in RFC 8547 and tcpcrypt, an encryption protocol to protect TCP streams, is described in RFC 8548. |
| Transport Layer Security (TLS) | TLS v1.0 is an IETF specification (RFC 2246) intended to replace SSL v3.0. TLS v1.0 employs Triple-DES (secret key cryptography), SHA (hash), Diffie-Hellman (key exchange), and DSS (digital signatures). TLS v1.0 was vulnerable to attack and updated by v1.1 (RFC 4346), which is now classified as an HISTORIC specification. TLS v1.1 was replaced by TLS v1.2 (RFC 5246) and, subsequently, by v1.3 (RFC 8446).
TLS is designed to operate over TCP. The IETF developed the Datagram Transport Layer Security (DTLS) protocol to operate over the User Datagram Protocol (UDP). DTLS v1.3 is described in RFC 9147. (See more detail about TLS below in Section 5.7.) |
| TrueCrypt | Open source, multi-platform cryptography software that can be used to encrypt a file, partition, or entire disk. One of TrueCrypt's more interesting features is that of plausible deniability with hidden volumes or hidden operating systems. The original Web site, truecrypt.org, suddenly went dark in May 2014. The current fork of TrueCrypt is VeraCrypt.
(See more detail about TrueCrypt below in Section 5.11.) |
| X.509 | ITU-T recommendation for the format of certificates for the public key infrastructure. Certificates map (bind) a user identity to a public key. The IETF application of X.509 certificates is documented in RFC 5280. An Internet X.509 Public Key Infrastructure is further defined in RFC 4210 (Certificate Management Protocols) and RFC 3647 (Certificate Policy and Certification Practices Framework). |
5.1. Password Protection
Nearly all modern multiuser computer and network operating systems employ passwords at the very least to protect and authenticate users accessing computer and/or network resources. But passwords are not typically kept on a host or server in plaintext, but are generally encrypted using some sort of hash scheme.
A) /etc/passwd file root:Jbw6BwE4XoUHo:0:0:root:/root:/bin/bash carol:FM5ikbQt1K052:502:100:Carol Monaghan:/home/carol:/bin/bash alex:LqAi7Mdyg/HcQ:503:100:Alex Insley:/home/alex:/bin/bash gary:FkJXupRyFqY4s:501:100:Gary Kessler:/home/gary:/bin/bash todd:edGqQUAaGv7g6:506:101:Todd Pritsky:/home/todd:/bin/bash josh:FiH0ONcjPut1g:505:101:Joshua Kessler:/home/webroot:/bin/bash B.1) /etc/passwd file (with shadow passwords) root:x:0:0:root:/root:/bin/bash carol:x:502:100:Carol Monaghan:/home/carol:/bin/bash alex:x:503:100:Alex Insley:/home/alex:/bin/bash gary:x:501:100:Gary Kessler:/home/gary:/bin/bash todd:x:506:101:Todd Pritsky:/home/todd:/bin/bash josh:x:505:101:Joshua Kessler:/home/webroot:/bin/bash B.2) /etc/shadow file root:AGFw$1$P4u/uhLK$l2.HP35rlu65WlfCzq:11449:0:99999:7::: carol:kjHaN%35a8xMM8a/0kMl1?fwtLAM.K&kw.:11449:0:99999:7::: alex:1$1KKmfTy0a7#3.LL9a8H71lkwn/.hH22a:11449:0:99999:7::: gary:9ajlknknKJHjhnu7298ypnAIJKL$Jh.hnk:11449:0:99999:7::: todd:798POJ90uab6.k$klPqMt%alMlprWqu6$.:11492:0:99999:7::: josh:Awmqpsui*787pjnsnJJK%aappaMpQo07.8:11492:0:99999:7::: FIGURE 8: Sample entries in Unix/Linux password files. |
Unix/Linux, for example, uses a well-known hash via its crypt() function. Passwords are stored in the /etc/passwd file (Figure 8A); each record in the file contains the username, hashed password, user's individual and group numbers, user's name, home directory, and shell program; these fields are separated by colons (:). Note that each password is stored as a 13-byte string. The first two characters are actually a salt, randomness added to each password so that if two users have the same password, they will still be encrypted differently; the salt, in fact, provides a means so that a single password might have 4096 different encryptions. The remaining 11 bytes are the password hash, calculated using DES.
As it happens, the /etc/passwd file is world-readable on Unix systems. This fact, coupled with the weak encryption of the passwords, resulted in the development of the shadow password system where passwords are kept in a separate, non-world-readable file used in conjunction with the normal password file. When shadow passwords are used, the password entry in /etc/passwd is replaced with a "*" or "x" (Figure 8B.1) and the MD5 hash of the passwords are stored in /etc/shadow along with some other account information (Figure 8B.2).
Windows NT uses a similar scheme to store passwords in the Security Access Manager (SAM) file. In the NT case, all passwords are hashed using the MD4 algorithm, resulting in a 128-bit (16-byte) hash value (they are then obscured using an undocumented mathematical transformation that was a secret until distributed on the Internet). The password password, for example, might be stored as the hash value (in hexadecimal) 60771b22d73c34bd4a290a79c8b09f18.
Passwords are not saved in plaintext on computer systems precisely so they cannot be easily compromised. For similar reasons, we don't want passwords sent in plaintext across a network. But for remote logon applications, how does a client system identify itself or a user to the server? One mechanism, of course, is to send the password as a hash value and that, indeed, may be done. A weakness of that approach, however, is that an intruder can grab the password off of the network and use an off-line attack (such as a dictionary attack where an attacker takes every known word and encrypts it with the network's encryption algorithm, hoping eventually to find a match with a purloined password hash). In some situations, an attacker only has to copy the hashed password value and use it later on to gain unauthorized entry without ever learning the actual password.
An even stronger authentication method uses the password to modify a shared secret between the client and server, but never allows the password in any form to go across the network. This is the basis for the Challenge Handshake Authentication Protocol (CHAP), the remote logon process used by Windows NT.
As suggested above, Windows NT passwords are stored in a security file on a server as a 16-byte hash value. In truth, Windows NT stores two hashes; a weak hash based upon the old LAN Manager (LanMan) scheme and the newer NT hash. When a user logs on to a server from a remote workstation, the user is identified by the username, sent across the network in plaintext (no worries here; it's not a secret anyway!). The server then generates a 64-bit random number and sends it to the client (also in plaintext). This number is the challenge.
Using the LanMan scheme, the client system then encrypts the challenge using DES. Recall that DES employs a 56-bit key, acts on a 64-bit block of data, and produces a 64-bit output. In this case, the 64-bit data block is the random number. The client actually uses three different DES keys to encrypt the random number, producing three different 64-bit outputs. The first key is the first seven bytes (56 bits) of the password's hash value, the second key is the next seven bytes in the password's hash, and the third key is the remaining two bytes of the password's hash concatenated with five zero-filled bytes. (So, for the example above, the three DES keys would be 60771b22d73c34, bd4a290a79c8b0, and 9f180000000000.) Each key is applied to the random number resulting in three 64-bit outputs, which comprise the response. Thus, the server's 8-byte challenge yields a 24-byte response from the client and this is all that would be seen on the network. The server, for its part, does the same calculation to ensure that the values match.
There is, however, a significant weakness to this system. Specifically, the response is generated in such a way as to effectively reduce 16-byte hash to three smaller hashes, of length seven, seven, and two, respectively. Thus, a password cracker has to break at most a 7-byte hash. One Windows NT vulnerability test program that I used in the past reported passwords that were "too short," defined as "less than 8 characters." When I asked how the program knew that passwords were too short, the software's salespeople suggested to me that the program broke the passwords to determine their length. This was, in fact, not the case at all; all the software really had to do was to look at the last eight bytes of the Windows NT LanMan hash to see that the password was seven or fewer characters.
Consider the following example, showing the LanMan hash of two different short passwords (take a close look at the last 8 bytes):
| AA: | 89D42A44E77140AAAAD3B435B51404EE |
| AAA: | 1C3A2B6D939A1021AAD3B435B51404EE |
Note that the NT hash provides no such clue:
| AA: | C5663434F963BE79C8FD99F535E7AAD8 |
| AAA: | 6B6E0FB2ED246885B98586C73B5BFB77 |
It is worth noting that the discussion above describes the Microsoft version of CHAP, or MS-CHAP (MS-CHAPv2 is described in RFC 2759). MS-CHAP assumes that it is working with hashed values of the password as the key to encrypting the challenge. More traditional CHAP (RFC 1994) assumes that it is starting with passwords in plaintext. The relevance of this observation is that a CHAP client, for example, cannot be authenticated by an MS-CHAP server; both client and server must use the same CHAP version.
5.2. Diffie-Hellman Key Exchange
Diffie and Hellman introduced the concept of public key cryptography. The mathematical "trick" of Diffie-Hellman key exchange is that it is relatively easy to compute exponents compared to computing discrete logarithms. Diffie-Hellman allows two parties — the ubiquitous Alice and Bob — to generate a secret key; they need to exchange some information over an unsecure communications channel to perform the calculation but an eavesdropper cannot determine the shared secret key based upon this information.
Diffie-Hellman works like this. Alice and Bob start by agreeing on a large prime number, N. They also have to choose some number G so that G<N.
There is actually another constraint on G, namely that it must be primitive with respect to N. Primitive is a definition that is a little beyond the scope of our discussion but basically G is primitive to N if the set of N-1 values of Gi mod N for i = (1,N-1) are all different. As an example, 2 is not primitive to 7 because the set of powers of 2 from 1 to 6, mod 7 (i.e., 21 mod 7, 22 mod 7, ..., 26 mod 7) = {2,4,1,2,4,1}. On the other hand, 3 is primitive to 7 because the set of powers of 3 from 1 to 6, mod 7 = {3,2,6,4,5,1}.
(The definition of primitive introduced a new term to some readers, namely mod. The phrase x mod y (and read as written!) means "take the remainder after dividing x by y." Thus, 1 mod 7 = 1, 9 mod 6 = 3, and 8 mod 8 = 0. Read more about the modulo function in the appendix.)
Anyway, either Alice or Bob selects N and G; they then tell the other party what the values are. Alice and Bob then work independently (Figure 9):
|
Note that XA and XB are kept secret while YA and YB are openly shared; these are the private and public keys, respectively. Based on their own private key and the public key learned from the other party, Alice and Bob have computed their secret keys, KA and KB, respectively, which are equal to GXAXB mod N.
Perhaps a small example will help here. Although Alice and Bob will really choose large values for N and G, I will use small values for example only; let's use N=7 and G=3, as shown in Figure 10.
|
In this example, then, Alice and Bob will both find the secret key 1 which is, indeed, 36 mod 7 (i.e., GXAXB = 32x3). If an eavesdropper (Eve) was listening in on the information exchange between Alice and Bob, she would learn G, N, YA, and YB which is a lot of information but insufficient to compromise the key; as long as XA and XB remain unknown, K is safe. As stated above, calculating Y = GX is a lot easier than finding X = logG Y.
A short digression on modulo arithmetic. In the paragraph above, we noted that 36 mod 7 = 1. This can be confirmed, of course, by noting that:
36 = 729 = 104*7 + 1
There is a nice property of modulo arithmetic, however, that makes this determination a little easier, namely: (a mod x)(b mod x) = (ab mod x). Therefore, one possible shortcut is to note that 36 = (33)(33). Therefore, 36 mod 7 = (33 mod 7)(33 mod 7) = (27 mod 7)(27 mod 7) = 6*6 mod 7 = 36 mod 7 = 1.
Diffie-Hellman can also be used to allow key sharing amongst multiple users. Note again that the Diffie-Hellman algorithm is used to generate secret keys, not to encrypt and decrypt messages.
5.3. RSA Public Key Cryptography
Unlike Diffie-Hellman, RSA can be used for key exchange as well as digital signatures and the encryption of small blocks of data. Today, RSA is primarily used to encrypt the session key used for secret key encryption (message integrity) or the message's hash value (digital signature). RSA's mathematical hardness comes from the ease in calculating large numbers and the difficulty in finding the prime factors of those large numbers. Although employed with numbers using hundreds of digits, the math behind RSA is relatively straight-forward.
To create an RSA public/private key pair, here are the basic steps:
- Choose two prime numbers, p and q. From these numbers you can calculate the modulus, n = pq.
- Select a third number, e, that is relatively prime to (i.e., it does not divide evenly into) the product (p-1)(q-1). The number e is the public exponent.
- Calculate an integer d from the quotient (ed-1)/[(p-1)(q-1)]. The number d is the private exponent.
The public key is the number pair (n,e). Although these values are publicly known, it is computationally infeasible to determine d from n and e if p and q are large enough.
To encrypt a message, M, with the public key, create the ciphertext, C, using the equation:
-
C = Me mod n
The receiver then decrypts the ciphertext with the private key using the equation:
-
M = Cd mod n
Now, this might look a bit complex and, indeed, the mathematics does take a lot of computer power given the large size of the numbers; since p and q may be 100 digits (decimal) or more, d and e will be about the same size and n may be over 200 digits. Nevertheless, a simple example may help. In this example, the values for p, q, e, and d are purposely chosen to be very small and the reader will see exactly how badly these values perform, but hopefully the algorithm will be adequately demonstrated:
- Select p=3 and q=5.
- The modulus n = pq = 15.
- The value e must be relatively prime to (p-1)(q-1) = (2)(4) = 8. Select e=11.
- The value d must be chosen so that (ed-1)/[(p-1)(q-1)] is an integer. Thus, the value (11d-1)/[(2)(4)] = (11d-1)/8 must be an integer. Calculate one possible value, d=3.
- Let's suppose that we want to send a message — maybe a secret key — that has the numeric value of 7 (i.e., M=7). [More on this choice below.]
- The sender encrypts the message (M) using the public key value (e,n)=(11,15) and computes the ciphertext (C) with the formula C = 711 mod 15 = 1977326743 mod 15 = 13.
- The receiver decrypts the ciphertext using the private key value (d,n)=(3,15) and computes the plaintext with the formula M = 133 mod 15 = 2197 mod 15 = 7.
I choose this trivial example because the value of n is so small (in particular, the value M cannot exceed n). But here is a more realistic example using larger d, e, and n values, as well as a more meaningful message; thanks to Barry Steyn for permission to use values from his How RSA Works With Examples page.
Let's say that we have chosen p and q so that we have the following value for n:
14590676800758332323018693934907063529240187237535716439958187
10198734387990053589383695714026701498021218180862924674228281
57022922076746906543401224889672472407926969987100581290103199
31785875366371086235765651050788371429711563734278891146353510
2712032765166518411726859837988672111837205085526346618740053
Let's also suppose that we have selected the public key, e, and private key, d, as follows:
65537
89489425009274444368228545921773093919669586065884257445497854
45648767483962981839093494197326287961679797060891728367987549
93315741611138540888132754881105882471930775825272784379065040
15680623423550067240042466665654232383502922215493623289472138
866445818789127946123407807725702626644091036502372545139713
Now suppose that our message (M) is the character string "attack at dawn" which has the numeric value (after converting the ASCII characters to a bit string and interpreting that bit string as a decimal number) of 1976620216402300889624482718775150.
The encryption phase uses the formula C = Me mod n, so C has the value:
35052111338673026690212423937053328511880760811579981620642802
34668581062310985023594304908097338624111378404079470419397821
53784997654130836464387847409523069325349451950801838615742252
26218879827232453912820596886440377536082465681750074417459151
485407445862511023472235560823053497791518928820272257787786
The decryption phase uses the formula M = Cd mod n, so M has the value that matches our original plaintext:
1976620216402300889624482718775150
This more realistic example gives just a clue as to how large the numbers are that are used in the real world implementations. RSA keylengths of 512 and 768 bits are considered to be pretty weak. The minimum suggested RSA key is 1024 bits; 2048 and 3072 bits are even better.
As an aside, Adam Back (http://www.cypherspace.org/~adam/) wrote a two-line Perl script to implement RSA. It employs dc, an arbitrary precision arithmetic package that ships with most UNIX systems:
print pack"C*",split/\D+/,`echo "16iII*o\U@{$/=$z;[(pop,pop,unpack"H*",<>
)]}\EsMsKsN0[lN*1lK[d2%Sa2/d0<X+d*lMLa^*lN%0]dsXx++lMlN/dsM0<J]dsJxp"|dc`
|
5.4. DES, Breaking DES, and DES Variants
The Data Encryption Standard (DES) started life in the mid-1970s, adopted by the National Bureau of Standards (NBS) [now the National Institute of Standards and Technology (NIST)] as Federal Information Processing Standard 46 (FIPS PUB 46-3) and by the American National Standards Institute (ANSI) as X3.92.
As mentioned earlier, DES uses the Data Encryption Algorithm (DEA), a secret key block-cipher employing a 56-bit key operating on 64-bit blocks. FIPS PUB 81 describes four modes of DES operation: Electronic Codebook (ECB), Cipher Block Chaining (CBC), Cipher Feedback (CFB), and Output Feedback (OFB). Despite all of these options, ECB is the most commonly deployed mode of operation.
NIST finally declared DES obsolete in 2004, and withdrew FIPS PUB 46-3, 74, and 81 (Federal Register, July 26, 2004, 69(142), 44509-44510). Although other block ciphers have replaced DES, it is still interesting to see how DES encryption is performed; not only is it sort of neat, but DES was the first crypto scheme commonly seen in non-governmental applications and was the catalyst for modern "public" cryptography and the first public Feistel cipher. DES still remains in many products — and cryptography students and cryptographers will continue to study DES for years to come.
DES Operational Overview
DES uses a 56-bit key. In fact, the 56-bit key is divided into eight 7-bit blocks and an 8th odd parity bit is added to each block (i.e., a "0" or "1" is added to the block so that there are an odd number of 1 bits in each 8-bit block). By using the 8 parity bits for rudimentary error detection, a DES key is actually 64 bits in length for computational purposes although it only has 56 bits worth of randomness, or entropy (See Section A.3 for a brief discussion of entropy and information theory).
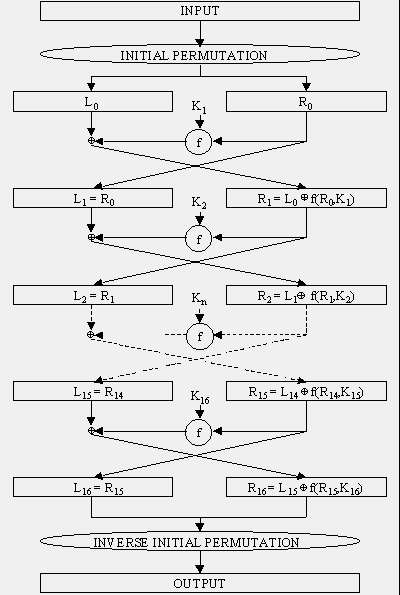
FIGURE 11: DES enciphering algorithm. |
DES then acts on 64-bit blocks of the plaintext, invoking 16 rounds of permutations, swaps, and substitutes, as shown in Figure 11. The standard includes tables describing all of the selection, permutation, and expansion operations mentioned below; these aspects of the algorithm are not secrets. The basic DES steps are:
- The 64-bit block to be encrypted undergoes an initial permutation (IP), where each bit is moved to a new bit position; e.g., the 1st, 2nd, and 3rd bits are moved to the 58th, 50th, and 42nd position, respectively.
- The 64-bit permuted input is divided into two 32-bit blocks, called left and right, respectively. The initial values of the left and right blocks are denoted L0 and R0.
- There are then 16 rounds of operation on the L and R blocks. During each iteration (where n ranges from 1 to 16), the following formulae apply:
-
Ln = Rn-1
Rn = Ln-1 ⊕ f(Rn-1,Kn)At any given step in the process, then, the new L block value is merely taken from the prior R block value. The new R block is calculated by taking the bit-by-bit exclusive-OR (XOR) of the prior L block with the results of applying the DES cipher function, f, to the prior R block and Kn. (Kn is a 48-bit value derived from the 64-bit DES key. Each round uses a different 48 bits according to the standard's Key Schedule algorithm.)
The cipher function, f, combines the 32-bit R block value and the 48-bit subkey in the following way. First, the 32 bits in the R block are expanded to 48 bits by an expansion function (E); the extra 16 bits are found by repeating the bits in 16 predefined positions. The 48-bit expanded R-block is then ORed with the 48-bit subkey. The result is a 48-bit value that is then divided into eight 6-bit blocks. These are fed as input into 8 selection (S) boxes, denoted S1,...,S8. Each 6-bit input yields a 4-bit output using a table lookup based on the 64 possible inputs; this results in a 32-bit output from the S-box. The 32 bits are then rearranged by a permutation function (P), producing the results from the cipher function.
- The results from the final DES round — i.e., L16 and R16 — are recombined into a 64-bit value and fed into an inverse initial permutation (IP-1). At this step, the bits are rearranged into their original positions, so that the 58th, 50th, and 42nd bits, for example, are moved back into the 1st, 2nd, and 3rd positions, respectively. The output from IP-1 is the 64-bit ciphertext block.
Consider this example using DES in CBC mode with the following 56-bit key and input:
-
Key: 1100101 0100100 1001001 0011101 0110101 0101011 1101100 0011010 = 0x6424491D352B6C1A
Input character string (ASCII/IA5): +2903015-08091765
Input string (hex): 0x2B323930333031352D3038303931373635
Output string (hex): 0x9812CB620B2E9FD3AD90DE2B92C6BBB6C52753AC43E1AFA6
Output character string (BASE64): mBLLYgsun9OtkN4rksa7tsUnU6xD4a+m
Observe that we start with a 17-byte input message. DES acts on eight bytes at a time, so this message is padded to 24 bytes and provides three "inputs" to the cipher algorithm (we don't see the padding here; it is appended by the DES code). Since we have three input blocks, we get 24 bytes of output from the three 64-bit (eight byte) output blocks.
If you want to test this, a really good free, online DES calculator hosted by the Information Security Group at University College London. An excellent step-by-step example of DES can also be found at J. Orlin Grabbe's The DES Algorithm Illustrated page.
NOTE: You'll notice that the output above is shown in BASE64. BASE64 is a 64-character alphabet — i.e., a six-bit character code composed of upper- and lower-case letters, the digits 0-9, and a few punctuation characters — that is commonly used as a way to display binary data. A byte has eight bits, or 256 values, but not all 256 ASCII characters are defined and/or printable. BASE64, simply, takes a binary string (or file), divides it into six-bit blocks, and translates each block into a printable character. More information about BASE64 can be found at my BASE64 Alphabet page or at Wikipedia.
Breaking DES
The mainstream cryptographic community has long held that DES's 56-bit key was too short to withstand a brute-force attack from modern computers. Remember Moore's Law: computer power doubles every 18 months. Given that increase in power, a key that could withstand a brute-force guessing attack in 1975 could hardly be expected to withstand the same attack a quarter century later.
DES is even more vulnerable to a brute-force attack because it is often used to encrypt words, meaning that the entropy of the 64-bit block is, effectively, greatly reduced. That is, if we are encrypting random bit streams, then a given byte might contain any one of 28 (256) possible values and the entire 64-bit block has 264, or about 18.5 quintillion, possible values. If we are encrypting words, however, we are most likely to find a limited set of bit patterns; perhaps 70 or so if we account for upper and lower case letters, the numbers, space, and some punctuation. This means that only about ¼ of the bit combinations of a given byte are likely to occur.
Despite this criticism, the U.S. government insisted throughout the mid-1990s that 56-bit DES was secure and virtually unbreakable if appropriate precautions were taken. In response, RSA Laboratories sponsored a series of cryptographic challenges to prove that DES was no longer appropriate for use.
DES Challenge I was launched in March 1997. It was completed in 84 days by R. Verser in a collaborative effort using thousands of computers on the Internet.
The first DES Challenge II lasted 40 days in early 1998. This problem was solved by distributed.net, a worldwide distributed computing network using the spare CPU cycles of computers around the Internet (participants in distributed.net's activities load a client program that runs in the background, conceptually similar to the SETI @Home "Search for Extraterrestrial Intelligence" project). The distributed.net systems were checking 28 billion keys per second by the end of the project.
The second DES Challenge II lasted less than 3 days. On July 17, 1998, the Electronic Frontier Foundation (EFF) announced the construction of hardware that could brute-force a DES key in an average of 4.5 days. Called Deep Crack, the device could check 90 billion keys per second and cost only about $220,000 including design (it was erroneously and widely reported that subsequent devices could be built for as little as $50,000). Since the design is scalable, this suggests that an organization could build a DES cracker that could break 56-bit keys in an average of a day for as little as $1,000,000. Information about the hardware design and all software can be obtained from the EFF.
The DES Challenge III, launched in January 1999, was broken is less than a day by the combined efforts of Deep Crack and distributed.net. This is widely considered to have been the final nail in DES's coffin.
The Deep Crack algorithm is actually quite interesting. The general approach that the DES Cracker Project took was not to break the algorithm mathematically but instead to launch a brute-force attack by guessing every possible key. A 56-bit key yields 256, or about 72 quadrillion, possible values. So the DES cracker team looked for any shortcuts they could find! First, they assumed that some recognizable plaintext would appear in the decrypted string even though they didn't have a specific known plaintext block. They then applied all 256 possible key values to the 64-bit block (I don't mean to make this sound simple!). The system checked to see if the decrypted value of the block was "interesting," which they defined as bytes containing one of the alphanumeric characters, space, or some punctuation. Since the likelihood of a single byte being "interesting" is about ¼, then the likelihood of the entire 8-byte stream being "interesting" is about ¼8, or 1/65536 (½16). This dropped the number of possible keys that might yield positive results to about 240, or about a trillion.
They then made the assumption that an "interesting" 8-byte block would be followed by another "interesting" block. So, if the first block of ciphertext decrypted to something interesting, they decrypted the next block; otherwise, they abandoned this key. Only if the second block was also "interesting" did they examine the key closer. Looking for 16 consecutive bytes that were "interesting" meant that only 224, or 16 million, keys needed to be examined further. This further examination was primarily to see if the text made any sense. Note that possible "interesting" blocks might be 1hJ5&aB7 or DEPOSITS; the latter is more likely to produce a better result. And even a slow laptop today can search through lists of only a few million items in a relatively short period of time. (Interested readers are urged to read Cracking DES and EFF's Cracking DES page.)
It is well beyond the scope of this paper to discuss other forms of breaking DES and other codes. Nevertheless, it is worth mentioning a couple of forms of cryptanalysis that have been shown to be effective against DES. Differential cryptanalysis, invented in 1990 by E. Biham and A. Shamir (of RSA fame), is a chosen-plaintext attack. By selecting pairs of plaintext with particular differences, the cryptanalyst examines the differences in the resultant ciphertext pairs. Linear plaintext, invented by M. Matsui, uses a linear approximation to analyze the actions of a block cipher (including DES). Both of these attacks can be more efficient than brute force.
DES Variants
Once DES was "officially" broken, several variants appeared. But none of them came overnight; work at hardening DES had already been underway. In the early 1990s, there was a proposal to increase the security of DES by effectively increasing the key length by using multiple keys with multiple passes. But for this scheme to work, it had to first be shown that the DES function is not a group, as defined in mathematics. If DES was a group, then we could show that for two DES keys, X1 and X2, applied to some plaintext (P), we can find a single equivalent key, X3, that would provide the same result; i.e.,
EX2(EX1(P)) = EX3(P)
where EX(P) represents DES encryption of some plaintext P using DES key X. If DES were a group, it wouldn't matter how many keys and passes we applied to some plaintext; we could always find a single 56-bit key that would provide the same result.
As it happens, DES was proven to not be a group so that as we apply additional keys and passes, the effective key length increases. One obvious choice, then, might be to use two keys and two passes, yielding an effective key length of 112 bits. Let's call this Double-DES. The two keys, Y1 and Y2, might be applied as follows:
C = EY2(EY1(P))
P = DY1(DY2(C))
where EY(P) and DY(C) represent DES encryption and decryption, respectively, of some plaintext P and ciphertext C, respectively, using DES key Y.
So far, so good. But there's an interesting attack that can be launched against this "Double-DES" scheme. First, notice that the applications of the formula above can be thought of with the following individual steps (where C' and P' are intermediate results):
C' = EY1(P) and C = EY2(C')
P' = DY2(C) and P = DY1(P')
Unfortunately, C'=P'. That leaves us vulnerable to a simple known plaintext attack (sometimes called "Meet-in-the-middle") where the attacker knows some plaintext (P) and its matching ciphertext (C). To obtain C', the attacker needs to try all 256 possible values of Y1 applied to P; to obtain P', the attacker needs to try all 256 possible values of Y2 applied to C. Since C'=P', the attacker knows when a match has been achieved — after only 256 + 256 = 257 key searches, only twice the work of brute-forcing DES. So "Double-DES" is not a good solution.
Triple-DES (3DES), based upon the Triple Data Encryption Algorithm (TDEA), is described in FIPS PUB 46-3. 3DES, which is not susceptible to a meet-in-the-middle attack, employs three DES passes and one, two, or three keys called K1, K2, and K3. Generation of the ciphertext (C) from a block of plaintext (P) is accomplished by:
C = EK3(DK2(EK1(P)))
where EK(P) and DK(P) represent DES encryption and decryption, respectively, of some plaintext P using DES key K. (For obvious reasons, this is sometimes referred to as an encrypt-decrypt-encrypt mode operation.)
Decryption of the ciphertext into plaintext is accomplished by:
P = DK1(EK2(DK3(C)))
The use of three, independent 56-bit keys provides 3DES with an effective key length of 168 bits. The specification also defines use of two keys where, in the operations above, K3 = K1; this provides an effective key length of 112 bits. Finally, a third keying option is to use a single key, so that K3 = K2 = K1 (in this case, the effective key length is 56 bits and 3DES applied to some plaintext, P, will yield the same ciphertext, C, as normal DES would with that same key). Given the relatively low cost of key storage and the modest increase in processing due to the use of longer keys, the best recommended practices are that 3DES be employed with three keys.
Another variant of DES, called DESX, is due to Ron Rivest. Developed in 1996, DESX is a very simple algorithm that greatly increases DES's resistance to brute-force attacks without increasing its computational complexity. In DESX, the plaintext input is XORed with 64 additional key bits prior to encryption and the output is likewise XORed with the 64 key bits. By adding just two XOR operations, DESX has an effective keylength of 120 bits against an exhaustive key-search attack. As it happens, DESX is no more immune to other types of more sophisticated attacks, such as differential or linear cryptanalysis, but brute-force is the primary attack vector on DES.
Closing Comments
After DES was deprecated and replaced by the Advanced Encryption Standard (AES) because of its vulnerability to a modestly-priced brute-force attack, many applications continued to rely on DES for security, and many software designers and implementers continued to include DES in new applications. In some cases, use of DES made sense but, inevitably, DES was discontinued in production software and hardware. RFC 4772 — dated December 2006 — discusses the security implications of employing DES, five years after AES had become the official standard.
On a final note, readers may be interested in seeing an Excel implementation of DES or J.O. Grabbe's The DES Algorithm Illustrated.
5.5. Pretty Good Privacy (PGP)
Pretty Good Privacy (PGP) is one of today's most widely used public key cryptography programs and was the first open cryptosystem that combined hashing, compression, SKC, and PKC into a method to protect files, devices, and e-mail. Public keys were shared via a concept known as a Web of Trust; individuals would directly exchange their public keyrings and then share their keyrings with other trusted parties. Developed by Philip Zimmermann in the early 1990s, and the subject of controversy for many years, PGP is available as a plug-in for many e-mail clients, such as Apple Mail (with GPG), Eudora, Gmail, Microsoft Outlook/Outlook Express, Mozilla Thunderbird (with Enigmail), and ProtonMail.
In June 1991, Zimmermann uploaded PGP to the Internet. PGP secret keys, however, were 128 bits or larger, making it a "strong" cryptography product. Export of strong crypto products without a license was a violation of International Traffic in Arms Regulations (ITAR) and, in fact, Zimmermann was the target of an FBI investigation from February 1993 to January 1996. Yet, in 1995, perhaps as a harbinger of the mixed feelings that this technology engendered, the Electronic Frontier Foundation (EFF) awarded Zimmermann the Pioneer Award and Newsweek Magazine named him one of the 50 most influential people on the Internet.
PGP can be used to sign or encrypt e-mail messages with the mere click of the mouse. Depending upon the version of PGP, the software uses SHA or MD5 for calculating the message hash; CAST, Triple-DES, or IDEA for encryption; and RSA or DSS/Diffie-Hellman for key exchange and digital signatures.
When PGP is first installed, the user has to create a key-pair. One key, the public key, can be advertised and widely circulated. The private key is protected by use of a passphrase. The passphrase has to be entered every time the user accesses their private key.
-----BEGIN PGP SIGNED MESSAGE----- Hash: SHA512 Hi Carol. What was that pithy Groucho Marx quote? /kess -----BEGIN PGP SIGNATURE----- Comment: GPGTools - https://gpgtools.org iQEcBAEBCgAGBQJYaTDaAAoJEE2ePRsA5fMj9wcH/jje/RBQYKg1ZYq1h52FpS3f GqnIkKq0wv2KiyCqIilbvb8eo2Fit7sIRo5AO3FJ9qIgRHvet+8pnRboks3uTYTM euNctkTOxcECZHupexdfB/5j5kGLn8UytIpHMa/Th4LKqvh+a6fU4nlCXe1qRSDq 7HUAvtG03LhPoAoVS411+wI+UtUf1+xvHLRJeKnhgi5j/d9tbc+K5rhPr8Bqb4Kz oHkGauPffRPfTsS+YpNoxg4eXMPBJprS9va8L2lCBPyUYEW77SSX/H2FHqPjVaxx /7j39Eu/oYtt5axnFBCYMZ2680kkFycd1RnCqhRJ8KZs6zhv3B8nQp6iS9dXrhg= =+mjr -----END PGP SIGNATURE----- FIGURE 12: A PGP signed message. The sender uses their private key to sign the message; at the destination, the sender's e-mail address yields the public key from the receiver's keyring in order to validate the signature. |
Figure 12 shows a PGP signed message. This message will not be kept secret from an eavesdropper, but a recipient can be assured that the message has not been altered from what the sender transmitted. In this instance, the sender signs the message using their own private key. The receiver uses the sender's public key to verify the signature; the public key is taken from the receiver's keyring based on the sender's e-mail address. Note that the signature process does not work unless the sender's public key is on the receiver's keyring.
-----BEGIN PGP MESSAGE----- Comment: GPGTools - https://gpgtools.org hQEMA02ePRsA5fMjAQf/fJIFvXKggtfaSAXJzRRZ3sXhKJN+0kH5Kj7GdqbhBd81 n0TZ31BAoXksEQ0Q3HbN8PbJ4qTwLE+glAqVqaGfGmieEirD74/6jX/jffuA028+ X110IX4gJTpkhHzYeabrxPy9yerjI2EQL0XI4313K7w4vKZ8kAEVU86+DCHKm3br B/UrYlYDPg2xPjgqIx8Zyga2fSnb4TvqYs2+6k9O7RHKu72wKY0H/xx+rqhEmEAk L/sIxrlCufVM22zEnlbhO5BEqRhBN6CkRS7HkvxOWHetw4dOIbCjc1WI2CMGzHoK Lx2a3wOskjFbS+0PnDU/CKJV002fO+MCxvYhsF3B7dLAFAG80+08XFBKMll99/Wj bttk96NLkaz45SG9KNJyqj7KaRFYscnUbEjHunvFIJCnl0CblJb3J/gBaa/ZbSLq 0GGDr9oc0tKoR97mabkyAhohcpiIn7f2y2aCBx5qTRT2uMiedmu4XtyktgB4LUo+ /MspTWlbcyKk9+Gx+9a7QaRkvBskwDn1wL/EIfNhXvtga+qGCV3rZwEX7f46jdzi NcptK7urvqiWgYtKS1z/0VrppbHBoTux3TQcFAEzKAGCYnS2YCyjNJRqTC/ODPE8 BIIYcYNq =+eqR -----END PGP MESSAGE----- FIGURE 13: A PGP encrypted message. The receiver's e-mail address is the pointer to the public key in the sender's keyring with which to encrypt the message. At the destination side, the receiver uses their own private key to decrypt the message. |
Figure 13 shows a PGP encrypted message (PGP compresses the file, where practical, prior to encryption because encrypted files have a high degree of randomness and, therefore, cannot be efficiently compressed). In this example, public key methods are used to exchange the session key for the actual message encryption that employs secret-key cryptography. In this case, the receiver's e-mail address is the pointer to the public key in the sender's keyring; in fact, the same message can be sent to multiple recipients and the message will not be significantly longer since all that needs to be added is the session key encrypted by each receiver's public key. When the message is received, the recipient will use their private key to extract the session secret key to successfully decrypt the message (Figure 14).
Hi Gary, "Outside of a dog, a book is man's best friend. Inside of a dog, it's too dark to read." Carol FIGURE 14: The decrypted message. |
It is worth noting that PGP was one of the first so-called "hybrid cryptosystems" that combined aspects of SKC and PKC. When Zimmermann was first designing PGP in the late-1980s, he wanted to use RSA to encrypt the entire message. The PCs of the days, however, suffered significant performance degradation when executing RSA so he hit upon the idea of using SKC to encrypt the message and PKC to encrypt the SKC key.
PGP went into a state of flux in 2002. Zimmermann sold PGP to Network Associates, Inc. (NAI) in 1997 and then resigned from NAI in early 2001. In March 2002, NAI announced that they were dropping support for the commercial version of PGP having failed to find a buyer for the product willing to pay what they wanted. In August 2002, PGP was purchased from NAI by PGP Corp. which, in turn, was purchased by Symantec. Meanwhile, there are many freeware versions of PGP available through the International PGP Page and the OpenPGP Alliance. OpenPGP is described more in RFC 9580.
The open-source programming GNU (an acronym for "GNU's Not Unix") project has developed GnuPG, aka GPG. For additional information, see the GNU Privacy Guard (GnuPG) and GPGTools Web pages.
5.6. IP Security (IPsec) Protocol
NOTE: The information in this section assumes that the reader is familiar with the Internet Protocol (IP), at least to the extent of the packet format and header contents. More information about IP can be found in An Overview of TCP/IP Protocols and the Internet. More information about IPv6 can be found in IPv6: The Next Generation Internet Protocol.
The Internet and the TCP/IP protocol suite were not built with security in mind. This is not meant as a criticism but as an observation; the baseline IP, TCP, UDP, and ICMP protocols were written in 1980 and built for the relatively closed ARPANET community. TCP/IP wasn't designed for the commercial-grade financial transactions that they now see or for virtual private networks (VPNs) on the Internet. To bring TCP/IP up to today's security necessities, the Internet Engineering Task Force (IETF) formed the IP Security Protocol Working Group which, in turn, developed the IP Security (IPsec) protocol. IPsec is not a single protocol, in fact, but a suite of protocols providing a mechanism to provide data integrity, authentication, privacy, and nonrepudiation for the classic Internet Protocol (IP). Although intended primarily for IP version 6 (IPv6), IPsec can also be employed by the current version of IP, namely IP version 4 (IPv4).
As shown in Table 3, IPsec is described in nearly a dozen RFCs. RFC 4301, in particular, describes the overall IP security architecture and RFC 2411 provides an overview of the IPsec protocol suite and the documents describing it.
IPsec can provide either message authentication and/or encryption. The latter requires more processing than the former, but will probably end up being the preferred usage for applications such as VPNs and secure electronic commerce.
Central to IPsec is the concept of a security association (SA). Authentication and confidentiality using AH or ESP use SAs and a primary role of IPsec key exchange it to establish and maintain SAs. An SA is a simplex (one-way or unidirectional) logical connection between two communicating IP endpoints that provides security services to the traffic carried by it using either AH or ESP procedures. The endpoint of an SA can be an IP host or IP security gateway (e.g., a proxy server, VPN server, etc.). Providing security to the more typical scenario of two-way (bi-directional) communication between two endpoints requires the establishment of two SAs (one in each direction).
An SA is uniquely identified by a 3-tuple composed of:
- Security Parameter Index (SPI), a 32-bit identifier of the connection
- IP Destination Address
- security protocol (AH or ESP) identifier
The IP Authentication Header (AH), described in RFC 4302, provides a mechanism for data integrity and data origin authentication for IP packets using HMAC with MD5 (RFC 2403 and RFC 6151), HMAC with SHA-1 (RFC 2404), or HMAC with RIPEMD (RFC 2857). See also RFC 4305.
0 1 2 3
0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 9 0 1
+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+
| Next Header | Payload Len | RESERVED |
+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+
| Security Parameters Index (SPI) |
+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+
| Sequence Number Field |
+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+
| |
+ Integrity Check Value-ICV (variable) |
| |
+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+
FIGURE 15: IPsec Authentication Header format. (From RFC 4302) |
Figure 15 shows the format of the IPsec AH. The AH is merely an additional header in a packet, more or less representing another protocol layer above IP (this is shown in Figure 17 below). Use of the IP AH is indicated by placing the value 51 (0x33) in the IPv4 Protocol or IPv6 Next Header field in the IP packet header. The AH follows mandatory IPv4/IPv6 header fields and precedes higher layer protocol (e.g., TCP, UDP) information. The contents of the AH are:
- Next Header: An 8-bit field that identifies the type of the next payload after the Authentication Header.
- Payload Length: An 8-bit field that indicates the length of AH in 32-bit words (4-byte blocks), minus "2". [The rationale for this is somewhat counter intuitive but technically important. All IPv6 extension headers encode the header extension length (Hdr Ext Len) field by first subtracting 1 from the header length, which is measured in 64-bit words. Since AH was originally developed for IPv6, it is an IPv6 extension header. Since its length is measured in 32-bit words, however, the Payload Length is calculated by subtracting 2 (32 bit words) to maintain consistency with IPv6 coding rules.] In the default case, the three 32-bit word fixed portion of the AH is followed by a 96-bit authentication value, so the Payload Length field value would be 4.
- Reserved: This 16-bit field is reserved for future use and always filled with zeros.
- Security Parameters Index (SPI): An arbitrary 32-bit value that, in combination with the destination IP address and security protocol, uniquely identifies the Security Association for this datagram. The value 0 is reserved for local, implementation-specific uses and values between 1-255 are reserved by the Internet Assigned Numbers Authority (IANA) for future use.
- Sequence Number: A 32-bit field containing a sequence number for each datagram; initially set to 0 at the establishment of an SA. AH uses sequence numbers as an anti-replay mechanism, to prevent a "person-in-the-middle" attack. If anti-replay is enabled (the default), the transmitted Sequence Number is never allowed to cycle back to 0; therefore, the sequence number must be reset to 0 by establishing a new SA prior to the transmission of the 232nd packet.
- Authentication Data: A variable-length, 32-bit aligned field containing the Integrity Check Value (ICV) for this packet (default length = 96 bits). The ICV is computed using the authentication algorithm specified by the SA, such as DES, MD5, or SHA-1. Other algorithms may also be supported.
The IP Encapsulating Security Payload (ESP), described in RFC 4303, provides message integrity and privacy mechanisms in addition to authentication. As in AH, ESP uses HMAC with MD5, SHA-1, or RIPEMD authentication (RFC 2403/RFC 2404/RFC 2857); privacy is provided using DES-CBC encryption (RFC 2405), NULL encryption (RFC 2410), other CBC-mode algorithms (RFC 2451), or AES (RFC 3686). See also RFC 4305 and RFC 4308.
0 1 2 3
0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 9 0 1
+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+ ----
| Security Parameters Index (SPI) | ^Int.
+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+ |Cov-
| Sequence Number | |ered
+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+ | ----
| Payload Data* (variable) | | ^
~ ~ | |
| | |Conf.
+ +-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+ |Cov-
| | Padding (0-255 bytes) | |ered*
+-+-+-+-+-+-+-+-+ +-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+ | |
| | Pad Length | Next Header | v v
+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+ ------
| Integrity Check Value-ICV (variable) |
~ ~
| |
+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+
* If included in the Payload field, cryptographic synchronization
data, e.g., an Initialization Vector (IV), usually is not
encrypted per se, although it often is referred to as being
being part of the ciphertext.
FIGURE 16: IPsec Encapsulating Security Payload format. (From RFC 4303) |
Figure 16 shows the format of the IPsec ESP information. Use of the IP ESP format is indicated by placing the value 50 (0x32) in the IPv4 Protocol or IPv6 Next Header field in the IP packet header. The ESP header (i.e., SPI and sequence number) follows mandatory IPv4/IPv6 header fields and precedes higher layer protocol (e.g., TCP, UDP) information. The contents of the ESP packet are:
- Security Parameters Index: (see description for this field in the AH, above.)
- Sequence Number: (see description for this field in the AH, above.)
- Payload Data: A variable-length field containing data as described by the Next Header field. The contents of this field could be encrypted higher layer data or an encrypted IP packet.
- Padding: Between 0 and 255 octets of padding may be added to the ESP packet. There are several applications that might use the padding field. First, the encryption algorithm that is used may require that the plaintext be a multiple of some number of bytes, such as the block size of a block cipher; in this case, the Padding field is used to fill the plaintext to the size required by the algorithm. Second, padding may be required to ensure that the ESP packet and resulting ciphertext terminate on a 4-byte boundary. Third, padding may be used to conceal the actual length of the payload. Unless another value is specified by the encryption algorithm, the Padding octets take on the value 1, 2, 3, ... starting with the first Padding octet. This scheme is used because, in addition to being simple to implement, it provides some protection against certain forms of "cut and paste" attacks.
- Pad Length: An 8-bit field indicating the number of bytes in the Padding field; contains a value between 0-255.
- Next Header: An 8-bit field that identifies the type of data in the Payload Data field, such as an IPv6 extension header or a higher layer protocol identifier.
- Authentication Data: (see description for this field in the AH, above.)
Two types of SAs are defined in IPsec, regardless of whether AH or ESP is employed. A transport mode SA is a security association between two hosts. Transport mode provides the authentication and/or encryption service to the higher layer protocol. This mode of operation is only supported by IPsec hosts. A tunnel mode SA is a security association applied to an IP tunnel. In this mode, there is an "outer" IP header that specifies the IPsec destination and an "inner" IP header that specifies the destination for the IP packet. This mode of operation is supported by both hosts and security gateways.
ORIGINAL PACKET BEFORE APPLYING AH
----------------------------
IPv4 |orig IP hdr | | |
|(any options)| TCP | Data |
----------------------------
---------------------------------------
IPv6 | | ext hdrs | | |
| orig IP hdr |if present| TCP | Data |
---------------------------------------
AFTER APPLYING AH (TRANSPORT MODE)
-------------------------------------------------------
IPv4 |original IP hdr (any options) | AH | TCP | Data |
-------------------------------------------------------
|<- mutable field processing ->|<- immutable fields ->|
|<----- authenticated except for mutable fields ----->|
------------------------------------------------------------
IPv6 | |hop-by-hop, dest*, | | dest | | |
|orig IP hdr |routing, fragment. | AH | opt* | TCP | Data |
------------------------------------------------------------
|<--- mutable field processing -->|<-- immutable fields -->|
|<---- authenticated except for mutable fields ----------->|
* = if present, could be before AH, after AH, or both
AFTER APPLYING AH (TUNNEL MODE)
----------------------------------------------------------------
IPv4 | | | orig IP hdr* | | |
|new IP header * (any options) | AH | (any options) |TCP| Data |
----------------------------------------------------------------
|<- mutable field processing ->|<------ immutable fields ----->|
|<- authenticated except for mutable fields in the new IP hdr->|
--------------------------------------------------------------
IPv6 | | ext hdrs*| | | ext hdrs*| | |
|new IP hdr*|if present| AH |orig IP hdr*|if present|TCP|Data|
--------------------------------------------------------------
|<--- mutable field -->|<--------- immutable fields -------->|
| processing |
|<-- authenticated except for mutable fields in new IP hdr ->|
* = if present, construction of outer IP hdr/extensions and
modification of inner IP hdr/extensions is discussed in
the Security Architecture document.
FIGURE 17: IPsec tunnel and transport modes for AH. (Adapted from RFC 4302) |
Figure 17 shows the IPv4 and IPv6 packet formats when using AH in both transport and tunnel modes. Initially, an IPv4 packet contains a normal IPv4 header (which may contain IP options), followed by the higher layer protocol header (e.g., TCP or UDP), followed by the higher layer data itself. An IPv6 packet is similar except that the packet starts with the mandatory IPv6 header followed by any IPv6 extension headers, and then followed by the higher layer data.
Note that in both transport and tunnel modes, the entire IP packet is covered by the authentication except for the mutable fields. A field is mutable if its value might change during transit in the network; IPv4 mutable fields include the fragment offset, time to live, and checksum fields. Note, in particular, that the address fields are not mutable.
ORIGINAL PACKET BEFORE APPLYING ESP
----------------------------
IPv4 |orig IP hdr | | |
|(any options)| TCP | Data |
----------------------------
---------------------------------------
IPv6 | | ext hdrs | | |
| orig IP hdr |if present| TCP | Data |
---------------------------------------
AFTER APPLYING ESP (TRANSPORT MODE)
-------------------------------------------------
IPv4 |orig IP hdr | ESP | | | ESP | ESP|
|(any options)| Hdr | TCP | Data | Trailer | ICV|
-------------------------------------------------
|<---- encryption ---->|
|<-------- integrity ------->|
---------------------------------------------------------
IPv6 | orig |hop-by-hop,dest*,| |dest| | | ESP | ESP|
|IP hdr|routing,fragment.|ESP|opt*|TCP|Data|Trailer| ICV|
---------------------------------------------------------
|<--- encryption ---->|
|<------ integrity ------>|
* = if present, could be before ESP, after ESP, or both
AFTER APPLYING ESP (TUNNEL MODE)
-----------------------------------------------------------
IPv4 | new IP hdr+ | | orig IP hdr+ | | | ESP | ESP|
|(any options)| ESP | (any options) |TCP|Data|Trailer| ICV|
-----------------------------------------------------------
|<--------- encryption --------->|
|<------------- integrity ------------>|
------------------------------------------------------------
IPv6 | new+ |new ext | | orig+|orig ext | | | ESP | ESP|
|IP hdr| hdrs+ |ESP|IP hdr| hdrs+ |TCP|Data|Trailer| ICV|
------------------------------------------------------------
|<--------- encryption ---------->|
|<------------ integrity ------------>|
+ = if present, construction of outer IP hdr/extensions and
modification of inner IP hdr/extensions is discussed in
the Security Architecture document.
FIGURE 18: IPsec tunnel and transport modes for ESP. (Adapted from RFC 4303) |
Figure 18 shows the IPv4 and IPv6 packet formats when using ESP in both transport and tunnel modes.
- As with AH, we start with a standard IPv4 or IPv6 packet.
- In transport mode, the higher layer header and data, as well as ESP trailer information, is encrypted and the entire ESP packet is authenticated. In the case of IPv6, some of the IPv6 extension options can precede or follow the ESP header.
- In tunnel mode, the original IP packet is encrypted and placed inside of an "outer" IP packet, while the entire ESP packet is authenticated.
Note a significant difference in the scope of ESP and AH. AH authenticates the entire packet transmitted on the network whereas ESP only covers a portion of the packet transmitted on the network (the higher layer data in transport mode and the entire original packet in tunnel mode). The reason for this is straight-forward; in AH, the authentication data for the transmission fits neatly into an additional header whereas ESP creates an entirely new packet which is the one encrypted and/or authenticated. But the ramifications are significant. ESP transport mode as well as AH in both modes protect the IP address fields of the original transmissions. Thus, using IPsec in conjunction with network address translation (NAT) might be problematic because NAT changes the values of these fields after IPsec processing.
The third component of IPsec is the establishment of security associations and key management. These tasks can be accomplished in one of two ways.
The simplest form of SA and key management is manual management. In this method, a security administer or other individual manually configures each system with the key and SA management data necessary for secure communication with other systems. Manual techniques are practical for small, reasonably static environments but they do not scale well.
For successful deployment of IPsec, however, a scalable, automated SA/key management scheme is necessary. Several protocols have defined for these functions:
- The Internet Security Association and Key Management Protocol (ISAKMP) defines procedures and packet formats to establish, negotiate, modify and delete security associations, and provides the framework for exchanging information about authentication and key management (RFC 2407/RFC 2408). ISAKMP's security association and key management is totally separate from key exchange.
- The OAKLEY Key Determination Protocol (RFC 2412) describes a scheme by which two authenticated parties can exchange key information. OAKLEY uses the Diffie-Hellman key exchange algorithm.
- The Internet Key Exchange (IKE) algorithm (RFC 2409) is the default automated key management protocol for IPsec.
- An alternative to IKE is Photuris (RFC 2522/RFC 2523), a scheme for establishing short-lived session-keys between two authenticated parties without passing the session-keys across the Internet. IKE typically creates keys that may have very long lifetimes.
5.7. Secure Transactions with SSL and TLS
The Secure Sockets Layer (SSL) protocol was developed by Netscape Communications to provide application-independent secure communication over the Internet for protocols such as the Hypertext Transfer Protocol (HTTP). SSL employs RSA and X.509 certificates during an initial handshake used to authenticate the server (client authentication is optional). The client and server then agree upon an encryption scheme. SSL v2.0 (1995), the first version publicly released, supported RC2 and RC4 with 40-bit keys. SSL v3.0 (1996) added support for DES, RC4 with a 128-bit key, and 3DES with a 168-bit key, all along with either MD5 or SHA-1 message hashes; this protocol is described in RFC 6101.

FIGURE 19: Browser encryption configuration screen (Firefox). |
In 1997, SSL v3 was found to be breakable. By this time, the Internet Engineering Task Force (IETF) had already started work on a new, non-proprietary protocol called Transport Layer Security (TLS), described in RFC 2246 (1999). TLS extends SSL and supports additional crypto schemes, such as Diffie-Hellman key exchange and DSS digital signatures; RFC 4279 describes the pre-shared key crypto schemes supported by TLS. TLS is backward compatible with SSL (and, in fact, is recognized as SSL v3.1). SSL v3.0 and TLS v1.0 are the commonly supported versions on servers and browsers today (Figure 19); SSL v2.0 is rarely found today and, in fact, RFC 6176-compliant clients and servers that support TLS will never negotiate the use of SSL v2.
In 2002, a cipher block chaining (CBC) vulnerability was described for TLS v1.0. In 2011, the theoretical became practical when a CBC proof-of-concept exploit was released. Meanwhile, TLS v1.1 was defined in 2006 (RFC 4346), adding protection against v1.0's CBC vulnerability. In 2008, TLS v1.2 was defined (RFC 5246), adding several additional cryptographic options. In 2018, TLS v1.3 was introduced (RFC 8446), adding clarification of acceptable crypto methods and better security.
Client Server
Key ^ ClientHello
Exch | + key_share*
| + signature_algorithms*
| + psk_key_exchange_modes*
v + pre_shared_key* -------->
ServerHello ^ Key
+ key_share* | Exch
+ pre_shared_key* v
{EncryptedExtensions} ^ Server
{CertificateRequest*} v Params
{Certificate*} ^
{CertificateVerify*} | Auth
{Finished} v
<-------- [Application Data*]
^ {Certificate*}
Auth | {CertificateVerify*}
v {Finished} -------->
[Application Data] <-------> [Application Data]
+ Indicates noteworthy extensions sent in the previously noted message.
* Indicates optional or situation-dependent messages/extensions that are not always sent.
{} Indicates messages protected using keys derived from a [sender]_handshake_traffic_secret.
[] Indicates messages protected using keys derived from [sender]_application_traffic_secret_N.
FIGURE 20: Basic TLS protocol handshake. (From RFC 8446)
|
The use of TLS is initiated when a user specifies the protocol https:// in a URL. The client (i.e., browser) will automatically try to make a TCP connection to the server at port 443 (unless another port is specified in the URL). The communication between the client and server comprises the TLS protocol handshake (Figure 20), which has three phases, followed by actual data exchange.
The first phase of the protocol handshake is Key Exchange, used to establish the shared key and select the encryption method. This is the only phase of TLS communication that is not encrypted. During this phase:
- The client sends a ClientHello message, composed of a random nonce, encryption protocols and versions that it can employ, and other parameters (and possible message extensions) required to negotiate the encryption protocol. (NOTE: One form of attack is to specify only old versions of protocols with known vulnerabilities and exploits. This is why servers are best advised to limit backward and downward compatibility.)
- The server responds with a ServerHello message, indicating the negotiated encryption and other connection parameters. The combination of these two "Hello" messages determines the shared encryption keys.
From this point forward, all communication is encrypted. The second step of the protocol handshake is the Server Parameters phase, where the server specifies other, additional handshake parameters. The server accomplishes this task by the use of two messages:
- The EncryptedExtensions message responds to any extensions that were included in the ClientHello message that were not required to determine the cryptographic parameters.
- A CertificateRequest message is only used if certificate-based client authentication is employed, in which case this message contains the desired parameters for that certificate.
The third, and final phase, of the TLS protocol handshake is Authentication, during which the server is authenticated (and, optionally, the client), keys are confirmed, and the integrity of the handshake assured. The messages exchanged during this phase include:
- A Certificate message contains the X.509 certificate of the sender (i.e., the client or the server). The server will not send this message if it is not authenticating with a certificate; the client will only send a certificate if the server sent a CertificateRequest during the Server Parameters phase of the protocol handshake.
- The CertificateVerify message contains a digital signature covering the entire protocol handshake exchange, employing the private key associated to the public key in the previously sent Certificate message. As above, this message is only sent by the client or server if they are employing certificate-based authentication.
- The Finished message contains a Message Authentication Code (MAC) over the entire handshake.
During this phase, the server sends its authentication messages followed by the client sending its authentication messages. Once the Finished messages have been exchanged, the protocol handshake is complete, and the client and server now start to exchange encrypted Application Data.
Side Note: It would probably be helpful to make some mention of how SSL/TLS is most commonly used today. Most of us have used SSL to engage in a secure, private transaction with some vendor. The steps are something like this. During the SSL exchange with the vendor's secure server, the server sends its certificate to our client software. The certificate includes the vendor's public key and a validation of some sort from the CA that issued the vendor's certificate (signed with the CA's private key). Our browser software is shipped with the major CAs' certificates containing their public keys; in that way, the client software can authenticate the server's certificate. Note that the server generally does not use a certificate to authenticate the client. Instead, purchasers are generally authenticated when a credit card number is provided; the server checks to see if the card purchase will be authorized by the credit card company and, if so, considers us valid and authenticated!
The reason that only the server is authenticated is rooted in history. SSL was developed to support e-commerce by providing a trust mechanism so that customers could have faith in a merchant. In the real world, you "trust" a store because you can walk into a brick-and-mortar structure. The store doesn't know who the customer is; they check to see if the credit card is valid and, if so, a purchase goes through. In e-commerce, we were trying to replicate the same experience — find a way in which the customer could trust the store and then make sure that the credit card was valid. In addition, how many people would have been willing to purchase an individual certificate and install it on their browser merely so that they shop online? This latter requirement, if implemented, could have killed e-commerce before it ever got started.
This all said, bidirectional — or mutual — authentication is supported by SSL, as noted in the figure above. See E. Cheng's "An Introduction to Mutual SSL Authentication" for an overview of how symmetric the process can be.
For historical purposes, it is worth mentioning Microsoft's Server Gated Cryptography (SGC) protocol, another (now long defunct) extension to SSL/TLS. For several decades, it had been illegal to generally export products from the U.S. that employed secret-key cryptography with keys longer than 40 bits. For that reason, during the 1996-1998 time period, browsers using SSL/TLS (e.g., Internet Explorer and Netscape Navigator) had an exportable version with weak (40-bit) keys and a domestic (North American) version with strong (128-bit) keys. By the late-1990s, products using strong SKC has been approved for the worldwide financial community. SGC was an extension to SSL that allowed financial institutions using Windows NT servers to employ strong cryptography. Both the client and server needed to have implemented SGC and the bank had to have a valid SGC certificate. During the initial handshake, the server would indicate support of SGC and supply its SGC certificate; if the client wished to use SGC and validated the server's SGC certificate, it would establish a secure session employing 128-bit RC2, 128-bit RC4, 56-bit DES, or 168-bit 3DES encryption. Microsoft supported SGC in the Windows 95/98/NT versions of Internet Explorer 4.0, Internet Information Server (IIS) 4.0, and Money 98.
As mentioned earlier, SSL was designed to provide application-independent transaction security for the Internet. Although the discussion above has focused on HTTP over SSL (https/TCP port 443), SSL can be used with several TCP/IP protocols (Table 4).
| Protocol | TCP Port Name/Number |
|---|---|
| File Transfer Protocol (FTP) | ftps-data/989 & ftps/990 |
| Hypertext Transfer Protocol (FTP) | https/443 |
| Internet Message Access Protocol v4 (IMAP4) | imaps/993 |
| Lightweight Directory Access Protocol (LDAP) | ldaps/636 |
| Network News Transport Protocol (NNTP) | nntps/563 |
| Post Office Protocol v3 (POP3) | pop3s/995 |
| Telnet | telnets/992 |
TLS was originally designed to operate over TCP. The IETF developed the Datagram Transport Layer Security (DTLS) protocol, based upon TLS, to operate over UDP. DTLS v1.3 is described in RFC 9147. (RFC 6347 defines DTLS v1.2 and DTLS v1.0 can be found in RFC 4347.) RFC 6655 describes a suite of AES in Counter with Cipher Block Chaining - Message Authentication Code (CBC-MAC) Mode (CCM) ciphers for use with TLS and DTLS. An interesting analysis of the TLS protocol can be found in the paper "Analysis and Processing of Cryptographic Protocols" by Cowie.

Vulnerabilities: A vulnerability in the OpenSSL Library was discovered in 2014. Known as Heartbleed, this vulnerability had apparently been introduced into OpenSSL in late 2011 with the introduction of a feature called heartbeat. Heartbleed exploited an implementation flaw in order to exfiltrate keying material from an SSL server (or some SSL clients, in what is known at reverse Heartbleed); the flaw allowed an attacker to grab 64 KB blocks from RAM. Heartbleed is known to only affect OpenSSL v1.0.1 through v1.0.1f; the exploit was patched in v1.0.1g. In addition, the OpenSSL 0.9.8 and 1.0.0 families are not vulnerable. Note also that Heartbleed affects some versions of the Android operating system, notably v4.1.0 and v4.1.1 (and some, possibly custom, implementations of v4.2.2). Note that Heartbleed did not exploit a flaw in the SSL protocol, but rather a flaw in the OpenSSL implementation.
But that wasn't the only problem with SSL. In October 2014, a new vulnerability was found called POODLE (Padding Oracle On Downgraded Legacy Encryption), a man-in-the-middle attack that exploited another SSL vulnerability that had unknowingly been in place for many years. Weeks later, an SSL vulnerability in the bash Unix command shell was discovered, aptly named Shellshock. (Here's a nice overview of the 2014 SSL problems!) In March 2015, the Bar Mitzvah Attack was exposed, exploiting a 13-year old vulnerability in the Rivest Cipher 4 (RC4) encryption algorithm. Then there was the FREAK (Factoring Attack on RSA-EXPORT Keys CVE-2015-0204) SSL/TLS Vulnerability that affected some SSL/TLS implementations, including Android OS and Chrome browser for OS X later that month.
In March 2016, the SSL DROWN (Decrypting RSA with Obsolete and Weakened eNcryption) attack was announced. DROWN works by exploiting the presence of SSLv2 to crack encrypted communications and steal information from Web servers, email servers, or VPN sessions. You might have read above that SSLv2 fell out of use by the early 2000s and was formally deprecated in 2011. This is true. But backward compatibility often causes old software to remain dormant and it seems that up to one-third of all HTTPS sites at the time were vulnerable to DROWN because SSLv2 had not been removed or disabled.
5.8. Elliptic Curve Cryptography (ECC)
In general, public key cryptography systems use hard-to-solve problems as the basis of the algorithm. The most predominant public key cryptography algorithm for many years was RSA, based on the prime factors of very large integers. While RSA can be successfully attacked, the mathematics of the algorithm have not been compromised, per se; instead, computational brute-force has broken the keys. The defense is "simple" — keep the size of the integer to be factored ahead of the computational curve!
In 1985, Elliptic Curve Cryptography (ECC) was proposed independently by cryptographers Victor Miller (IBM) and Neal Koblitz (University of Washington). ECC is based on the difficulty of solving the Elliptic Curve Discrete Logarithm Problem (ECDLP). Like the prime factorization problem, ECDLP is another "hard" problem that is deceptively simple to state: Given two points, P and Q, on an elliptic curve, find the integer n, if it exists, such that Q = nP.
The first thing to note about elliptic curves is that they are neither elliptic (i.e., they are not an oval or ellipse) nor are they curves (i.e., they are not curves in common meaning, which are merely bent lines). Elliptic curves are a part of number theory and algebraic geometry, and can be defined over any field of numbers (i.e., real, integer, complex, etc.). In cryptography, we normally use elliptic curves over a finite field of prime numbers, which we denote FP. This is one reason that we use the modulo function; modulo arithmetic defines a finite range of numbers (e.g., 0 to N-1 if using modulo N) which will, in turn, yield a finite number of primes.
So, given this preamble, an elliptic curve in FP consists of the set of real numbers (x,y) that satisfies the equation:
y2 = (x3 + ax + b) modulo N
In addition, the curve has to be non-singular (sometimes stated as "not containing any singularities"), which means that the curve has no cusps, self-intersections, or isolated points. To ensure this, there is one more condition, namely, the values of a and b must satisfy the requirement that:
4a3 + 27b2 ≠ 0
The set of all of the solutions to the equation forms the elliptic curve. Changing a and b changes the shape of the curve, and small changes in these parameters can result in major changes in the set of (x,y) solutions. The ECC standards documents list a host of ECC curves and they differ by changing these parameters.
FIGURE 21: Elliptic curve addition. (Source: Dams, 2012) |
Figure 21 shows the addition of two points on the elliptic curve where a = -3 and b = 5. Elliptic curves have the interesting property that adding two points on the elliptic curve yields a third point on the curve. Therefore, adding two points, P and Q, gets us to point R. Small changes in P or Q can cause a large change in the position of R.
Now, the astute reader will notice that the line above went through a point labelled -R and that, in the Cartesian coordinate system, we've merely changed the sign of the y coordinate to get the point labelled R; i.e., we've "reflected" the point around the x-axis. It turns out that it doesn't matter because the curve is solving the equation for y2, meaning that if a point exists in the +y space, the same point exists in the -y space because (+y)2 = (-y)2. Stated another, slightly more rigorous way, the curve is symmetric about the x-axis.
So, if it doesn't matter, why do it? Remember that our original problem was to find Q = nP. So, to get there, we need to define a number of operations on P, including doubling P and multiplying P by some number. At this point, we leave the area of simple scalar arithmetic and enter into group law and algebraic geometry. There are a bunch of good explanations about why we do this reflection that I am not going to replicate but I will give one key thing to keep in mind. While the sign doesn't matter when squaring a number, it does matter in other types of arithmetic. When adding points on the elliptic curve, we need to maintain the associative law, which says:
(A + B) + C = A + (B + C)
Working with elliptic curves gets us into group laws and the operations often reflect about the x-axis in order to maintain the associative principle. In any case, there's a pretty good discussion about this on StackExchange and in "The group law" section on the ECC Wikipedia page.
So let's go back to the original problem statement from above. The point Q is calculated as a multiple of the starting point, P, or, Q = nP. An attacker might know P and Q but finding the integer, n, is a difficult problem to solve. Q (i.e., nP) is the public key and n is the private key.
ECC may be employed with many Internet standards, including CCITT X.509 certificates and certificate revocation lists (CRLs), Internet Key Exchange (IKE), Transport Layer Security (TLS), XML signatures, and applications or protocols based on the cryptographic message syntax (CMS). ANSI, IEEE, IETF, NIST, the Standards for Efficient Cryptography Group (SECG), and others have also defined "safe curves" for use in various applications for ECC, such as:
- RFC 5639: Elliptic Curve Cryptography (ECC) Brainpool Standard Curves and Curve Generation (2010)
- RFC 6637: Elliptic Curve Cryptography (ECC) in OpenPGP (2012) proposes additional elliptic curves for use with OpenPGP (e.g., NIST's FIPS PUB 186-4: Digital Signature Standard (DSS) [NIST, 2013]
- SEC 2: Recommended Elliptic Curve Domain Parameters (SECG, 2010)
See Bernstein and Lange's SafeCurves: choosing safe curves for elliptic-curve cryptography site for a review and analysis of various ECC curve standard specifications.
| ECC Key Size | RSA Key Size | Key-Size Ratio |
AES Key Size |
|---|---|---|---|
| 160 | 1,024 | 1:6 | n/a |
| 256 | 3,072 | 1:12 | 128 |
| 384 | 7,680 | 1:20 | 192 |
| 512 | 15,360 | 1:30 | 256 |
| Key sizes in bits. | |||
RSA had been the mainstay of PKC since its development in the late 1970s. ECC has emerged as a replacement in many environments because it provides similar levels of security compared to RSA but with significantly reduced key sizes and, therefore, reduced processing demands. Table 5 shows the key size relationship between ECC and RSA, and the appropriate choice of AES key size.
Since the ECC key sizes are so much shorter than comparable RSA keys, the length of the public key and private key is much shorter in elliptic curve cryptosystems. This results into faster processing times, and lower demands on memory and bandwidth; some studies have found that ECC is faster than RSA for signing and decryption, but slower for signature verification and encryption. ECC is particularly useful in applications where memory, bandwidth, and/or computational power is limited (e.g., a smartcard or smart device) and it is in this area that ECC use has been growing.
There are a number of exceptional ECC tutorials online at various levels of detail and complexity to which readers are referred:
- Elliptic Curve Cryptography (Bauer)
- "ECCHacks: a gentle introduction to elliptic-curve cryptography" (Bernstein & Lange)
- ECC Tutorial (Certicom)
- An Introduction to Elliptic Curve Cryptography (Dams) [See also embedded.com]
- A (Relatively Easy To Understand) Primer on Elliptic Curve Cryptography (Sullivan)
- Elliptic-curve cryptography (Wikipedia)
5.9. The Advanced Encryption Standard (AES) and Rijndael
The search for a replacement to DES started in January 1997 when NIST announced that it was looking for an Advanced Encryption Standard. In September of that year, they put out a formal Call for Algorithms and in August 1998 announced that 15 candidate algorithms were being considered (Round 1). In April 1999, NIST announced that the 15 had been whittled down to five finalists (Round 2): MARS (multiplication, addition, rotation and substitution) from IBM; Ronald Rivest's RC6; Rijndael from a Belgian team; Serpent, developed jointly by a team from England, Israel, and Norway; and Twofish, developed by Bruce Schneier. In October 2000, NIST announced their selection: Rijndael.
The remarkable thing about this entire process has been the openness as well as the international nature of the "competition." NIST maintained an excellent Web site devoted to keeping the public fully informed, at http://csrc.nist.gov/archive/aes/, which is now available as an archive site. Their Overview of the AES Development Effort has full details of the process, algorithms, and comments so I will not repeat everything here.
In October 2000, NIST released the Report on the Development of the Advanced Encryption Standard (AES) that compared the five Round 2 algorithms in a number of categories. Table 6 summarizes the relative scores of the five schemes (1=low, 3=high):
| Algorithm | |||||
|---|---|---|---|---|---|
| Category | MARS | RC6 | Rijndael | Serpent | Twofish |
| General security | 3 | 2 | 2 | 3 | 3 |
| Implementation of security | 1 | 1 | 3 | 3 | 2 |
| Software performance | 2 | 2 | 3 | 1 | 1 |
| Smart card performance | 1 | 1 | 3 | 3 | 2 |
| Hardware performance | 1 | 2 | 3 | 3 | 2 |
| Design features | 2 | 1 | 2 | 1 | 3 |
With the report came the recommendation that Rijndael be named as the AES standard. In February 2001, NIST released the Draft Federal Information Processing Standard (FIPS) AES Specification for public review and comment. AES contains a subset of Rijndael's capabilities (e.g., AES only supports a 128-bit block size) and uses some slightly different nomenclature and terminology, but to understand one is to understand both. The 90-day comment period ended on May 29, 2001 and the U.S. Department of Commerce officially adopted AES in December 2001, published as FIPS PUB 197.
AES (Rijndael) Overview
Rijndael (pronounced as in "rain doll" or "rhine dahl") is a block cipher designed by Joan Daemen and Vincent Rijmen, both cryptographers in Belgium. Rijndael can operate over a variable-length block using variable-length keys; the specification submitted to NIST describes use of a 128-, 192-, or 256-bit key to encrypt data blocks that are 128, 192, or 256 bits long; note that all nine combinations of key length and block length are possible. The algorithm is written in such a way that block length and/or key length can easily be extended in multiples of 32 bits and it is specifically designed for efficient implementation in hardware or software on a range of processors. The design of Rijndael was strongly influenced by the block cipher called Square, also designed by Daemen and Rijmen.
Rijndael is an iterated block cipher, meaning that the initial input block and cipher key undergoes multiple rounds of transformation before producing the output. Each intermediate cipher result is called a State.
For ease of description, the block and cipher key are often represented as an array of columns where each array has 4 rows and each column represents a single byte (8 bits). The number of columns in an array representing the state or cipher key, then, can be calculated as the block or key length divided by 32 (32 bits = 4 bytes). An array representing a State will have Nb columns, where Nb values of 4, 6, and 8 correspond to a 128-, 192-, and 256-bit block, respectively. Similarly, an array representing a Cipher Key will have Nk columns, where Nk values of 4, 6, and 8 correspond to a 128-, 192-, and 256-bit key, respectively. An example of a 128-bit State (Nb=4) and 192-bit Cipher Key (Nk=6) is shown below:
|
|
The number of transformation rounds (Nr) in Rijndael is a function of the block length and key length, and is shown in Table 7.
| No. of Rounds Nr |
Block Size | |||
|---|---|---|---|---|
| 128 bits Nb = 4 |
192 bits Nb = 6 |
256 bits Nb = 8 | ||
| Key Size |
128 bits Nk = 4 |
10 | 12 | 14 |
| 192 bits Nk = 6 |
12 | 12 | 14 | |
| 256 bits Nk = 8 |
14 | 14 | 14 | |
Now, having said all of this, the AES version of Rijndael does not support all nine combinations of block and key lengths, but only the subset using a 128-bit block size. NIST calls these supported variants AES-128, AES-192, and AES-256 where the number refers to the key size. Table 8 shows the Nb, Nk, and Nr values supported in AES.
| Parameters | |||
|---|---|---|---|
| Variant | Nb | Nk | Nr |
| AES-128 | 4 | 4 | 10 |
| AES-192 | 4 | 6 | 12 |
| AES-256 | 4 | 8 | 14 |
The AES/Rijndael cipher itself has three operational stages:
- AddRound Key transformation
- Nr-1 Rounds comprising:
- SubBytes transformation
- ShiftRows transformation
- MixColumns transformation
- AddRoundKey transformation
- A final Round comprising:
- SubBytes transformation
- ShiftRows transformation
- AddRoundKey transformation
The paragraphs below will describe the operations mentioned above. The nomenclature used below is taken from the AES specification although references to the Rijndael specification are made for completeness. The arrays s and s' refer to the State before and after a transformation, respectively (NOTE: The Rijndael specification uses the array nomenclature a and b to refer to the before and after States, respectively). The subscripts i and j are used to indicate byte locations within the State (or Cipher Key) array.
The SubBytes transformation
The substitute bytes (called ByteSub in Rijndael) transformation operates on each of the State bytes independently and changes the byte value. An S-box, or substitution table, controls the transformation. The characteristics of the S-box transformation as well as a compliant S-box table are provided in the AES specification; as an example, an input State byte value of 107 (0x6b) will be replaced with a 127 (0x7f) in the output State and an input value of 8 (0x08) would be replaced with a 48 (0x30).
One way to think of the SubBytes transformation is that a given byte in State s is given a new value in State s' according to the S-box. The S-box, then, is a function on a byte in State s so that:
s'i,j = S-box (si,j)
The more general depiction of this transformation is shown by:
|
|
|
|
|
The ShiftRows transformation
The shift rows (called ShiftRow in Rijndael) transformation cyclically shifts the bytes in the bottom three rows of the State array. According to the more general Rijndael specification, rows 2, 3, and 4 are cyclically left-shifted by C1, C2, and C3 bytes, respectively, as shown below:
| Nb | C1 | C2 | C3 |
|---|---|---|---|
| 4 | 1 | 2 | 3 |
| 6 | 1 | 2 | 3 |
| 8 | 1 | 3 | 4 |
The current version of AES, of course, only allows a block size of 128 bits (Nb = 4) so that C1=1, C2=2, and C3=3. The diagram below shows the effect of the ShiftRows transformation on State s:
|
|
|
The MixColumns transformation
The mix columns (called MixColumn in Rijndael) transformation uses a mathematical function to transform the values of a given column within a State, acting on the four values at one time as if they represented a four-term polynomial. In essence, if you think of MixColumns as a function, this could be written:
s'i,c = MixColumns (si,c)
for 0 ≤ i ≤ 3 for some column, c. The column position doesn't change, merely the values within the column.
Round Key generation and the AddRoundKey transformation
The AES Cipher Key can be 128, 192, or 256 bits in length. The Cipher Key is used to derive a different key to be applied to the block during each round of the encryption operation. These keys are called the Round Keys and each will be the same length as the block, i.e., Nb 32-bit words (words will be denoted W).
The AES specification defines a key schedule by which the original Cipher Key (of length Nk 32-bit words) is used to form an Expanded Key. The Expanded Key size is equal to the block size times the number of encryption rounds plus 1, which will provide Nr+1 different keys. (Note that there are Nr encipherment rounds but Nr+1 AddRoundKey transformations.)
Consider that AES uses a 128-bit block and either 10, 12, or 14 iterative rounds depending upon key length. With a 128-bit key, for example, we would need 1408 bits of key material (128x11=1408), or an Expanded Key size of 44 32-bit words (44x32=1408). Similarly, a 192-bit key would require 1664 bits of key material (128x13), or 52 32-bit words, while a 256-bit key would require 1920 bits of key material (128x15), or 60 32-bit words. The key expansion mechanism, then, starts with the 128-, 192-, or 256-bit Cipher Key and produces a 1408-, 1664-, or 1920-bit Expanded Key, respectively. The original Cipher Key occupies the first portion of the Expanded Key and is used to produce the remaining new key material.
The result is an Expanded Key that can be thought of and used as 11, 13, or 15 separate keys, each used for one AddRoundKey operation. These, then, are the Round Keys. The diagram below shows an example using a 192-bit Cipher Key (Nk=6), shown in magenta italics:
| Expanded Key: | W0 | W1 | W2 | W3 | W4 | W5 | W6 | W7 | W8 | W9 | W10 | W11 | W12 | W13 | W14 | W15 | ... | W44 | W45 | W46 | W47 | W48 | W49 | W50 | W51 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Round keys: | Round key 0 | Round key 1 | Round key 2 | Round key 3 | ... | Round key 11 | Round key 12 | ||||||||||||||||||
The AddRoundKey (called Round Key addition in Rijndael) transformation merely applies each Round Key, in turn, to the State by a simple bit-wise exclusive OR operation. Recall that each Round Key is the same length as the block.
Summary
Ok, I hope that you've enjoyed reading this as much as I've enjoyed writing it — and now let me guide you out of the microdetail! Recall from the beginning of the AES overview that the cipher itself comprises a number of rounds of just a few functions:
- SubBytes takes the value of a word within a State and substitutes it with another value by a predefined S-box
- ShiftRows circularly shifts each row in the State by some number of predefined bytes
- MixColumns takes the value of a 4-word column within the State and changes the four values using a predefined mathematical function
- AddRoundKey XORs a key that is the same length as the block, using an Expanded Key derived from the original Cipher Key
Cipher (byte in[4*Nb], byte out[4*Nb], word w[Nb*(Nr+1)])
begin
byte state[4,Nb]
state = in
AddRoundKey(state, w)
for round = 1 step 1 to Nr-1
SubBytes(state)
ShiftRows(state)
MixColumns(state)
AddRoundKey(state, w+round*Nb)
end for
SubBytes(state)
ShiftRows(state)
AddRoundKey(state, w+Nr*Nb)
out = state
end
FIGURE 22: AES pseudocode.
|
As a last and final demonstration of the operation of AES, Figure 22 is a pseudocode listing for the operation of the AES cipher. In the code:
- in[] and out[] are 16-byte arrays with the plaintext and cipher text, respectively. (According to the specification, both of these arrays are actually 4*Nb bytes in length but Nb=4 in AES.)
- state[] is a 2-dimensional array containing bytes in 4 rows and 4 columns. (According to the specification, this arrays is 4 rows by Nb columns.)
- w[] is an array containing the key material and is 4*(Nr+1) words in length. (Again, according to the specification, the multiplier is actually Nb.)
- AddRoundKey(), SubBytes(), ShiftRows(), and MixColumns() are functions representing the individual transformations.
5.10. Cisco's Stream Cipher
Stream ciphers take advantage of the fact that:
x ⊕ y ⊕ y = x
One of the encryption schemes employed by Cisco routers to encrypt passwords is a stream cipher. It uses the following fixed keystream (thanks also to Jason Fossen for independently extending and confirming this string):
dsfd;kfoA,.iyewrkldJKDHSUBsgvca69834ncx
When a password is to be encrypted, the password function chooses a number between 0 and 15, and that becomes the offset into the keystream. Password characters are then XORed byte-by-byte with the keystream according to:
Ci = Pi ⊕ K(offset+i)
where K is the keystream, P is the plaintext password, and C is the ciphertext password.
Consider the following example. Suppose we have the password abcdefgh. Converting the ASCII characters yields the hex string 0x6162636465666768.
The keystream characters and hex code that supports an offset from 0 to 15 bytes and a password length up to 24 bytes is:
d s f d ; k f o A , . i y e w r k l d J K D H S U B s g v c a 6 9 8 3 4 n c x
0x647366643b6b666f412c2e69796577726b6c644a4b4448535542736776636136393833346e6378
Let's say that the function decides upon a keystream offset of 6 bytes. We then start with byte 6 of the keystream (start counting the offset at 0) and XOR with the password:
0x666f412c2e697965
⊕ 0x6162636465666768
------------------
0x070D22484B0F1E0D
The password would now be displayed in the router configuration as:
password 7 06070D22484B0F1E0D
where the "7" indicates the encryption type, the leading "06" indicates the offset into the keystream, and the remaining bytes are the encrypted password characters.
(Decryption is pretty trivial so that exercise is left to the reader. If you need some help with byte-wise XORing, see http://www.garykessler.net/library/byte_logic_table.html. If you'd like some programs that do this, see http://www.garykessler.net/software/index.html#cisco7.)
5.11. TrueCrypt
TrueCrypt is an open source, on-the-fly crypto system that can be used on devices supports by Linux, MacOS, and Windows. First released in 2004, TrueCrypt can be employed to encrypt a partition on a disk or an entire disk.
On May 28, 2014, the TrueCrypt.org Web site was suddenly taken down and redirected to the SourceForge page. Although this paper is intended as a crypto tutorial and not a news source about crypto controversy, the sudden withdrawal of TrueCrypt cannot go without notice. The last stable release of TrueCrypt is v7.1a (February 2012); v7.2, released on May 28, 2014, only decrypts TrueCrypt volumes, ostensibly so that users can migrate to another solution. The TrueCryptNext (TCnext) Web page quickly went online at TrueCrypt.ch, using the tag line "TrueCrypt will not die" and noting that independent hosting in Switzerland guaranteed no product development interruption due to legal threats. The TCnext site became a repository of TrueCrypt v7.1a downloads and never released any subsequent software. The TrueCrypt Wikipedia page and accompanying references have some good information about the "end" of TrueCrypt as we knew it.
While there did not appear to be any rush to abandon TrueCrypt, it was also the case that you don't want to use old, unsupported software for too long. Another replacement was announced almost immediately upon the demise of TrueCrypt: "TrueCrypt may live on after all as CipherShed." The CipherShed group never produced a product, however, and the CipherShed Web site no longer appeared to be operational sometime after October 2016. The only current, working fork of TrueCrypt appears to be VeraCrypt, which is also open source, multi-platform, operationally identical to TrueCrypt, and compatible with TrueCrypt containers.
One final editorial comment. TrueCrypt was not broken or otherwise compromised. It was withdrawn by its developers for reasons that have not yet been made public but there is no evidence to assume that TrueCrypt has been damaged in any way; on the contrary, two audits, completed in April 2014 and April 2015, found no evidence of backdoors or malicious code. See Steve Gibson's TrueCrypt: Final Release Repository page for more information!
TrueCrypt uses a variety of encryption schemes, including AES, Serpent, and Twofish. A TrueCrypt volume is stored as a file that appears to be filled with random data, thus has no specific file signature. (It is true that a TrueCrypt container will pass a chi-square (Χ2) randomness test, but that is merely a general indicator of possibly encrypted content. An additional clue is that a TrueCrypt container will also appear on a disk as a file that is some increment of 512 bytes in size. While these indicators might raise a red flag, they don't rise to the level of clearly identifying a TrueCrypt volume.)
When a user creates a TrueCrypt volume, a number of parameters need to be defined, such as the size of the volume and the password. To access the volume, the TrueCrypt program is employed to find the TrueCrypt encrypted file, which is then mounted as a new drive on the host system.

FIGURE 23: TrueCrypt screen shot (Windows). |
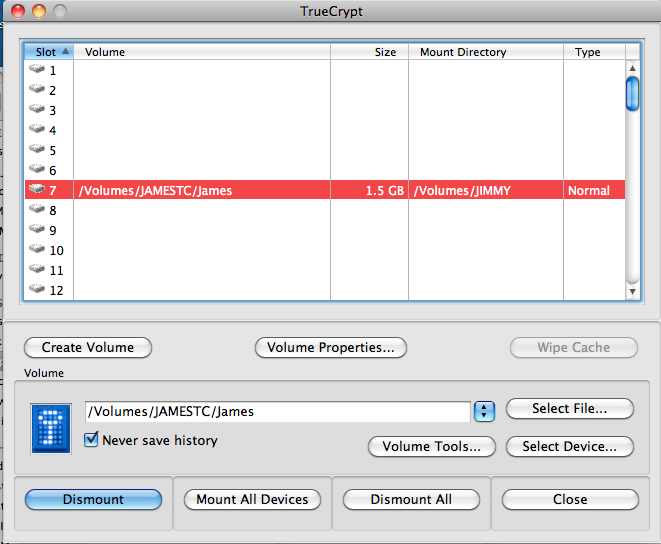
FIGURE 24: TrueCrypt screen shot (MacOS). |
Consider this example where an encrypted TrueCrypt volume is stored as a file named James on a thumb drive. On a Windows system, this thumb drive has been mounted as device E:. If one were to view the E: device, any number of files might be found. The TrueCrypt application is used to mount the TrueCrypt file; in this case, the user has chosen to mount the TrueCrypt volume as device K: (Figure 23). Alternatively, the thumb drive could be used with a Mac system, where it has been mounted as the /Volumes/JIMMY volume. TrueCrypt mounts the encrypted file, James, and it is now accessible to the system (Figure 24).
 FIGURE 25: TrueCrypt hidden encrypted volume within an encrypted volume. (From http://www.truecrypt.org/images/docs/hidden-volume.gif) |
One of the most interesting — certainly one of the most controversial — features of TrueCrypt is called plausible deniability, protection in case a user is "compelled" to turn over the encrypted volume's password. When the user creates a TrueCrypt volume, he/she chooses whether to create a standard or hidden volume. A standard volume has a single password, while a hidden volume is created within a standard volume and uses a second password. As shown in Figure 25, the unallocated (free) space in a TrueCrypt volume is always filled with random data, thus it is impossible to differentiate a hidden encrypted volume from a standard volume's free space.
To access the hidden volume, the file is mounted as shown above and the user enters the hidden volume's password. When under duress, the user would merely enter the password of the standard (i.e., non-hidden) TrueCrypt volume.
More information about TrueCrypt can be found at the TCnext Web Site or in the TrueCrypt User's Guide (v7.1a).
An active area of research in the digital forensics community is to find methods with which to detect hidden TrueCrypt volumes. Most of the methods do not detect the presence of a hidden volume, per se, but infer the presence by left over forensic remnants. As an example, both MacOS and Windows systems usually have a file or registry entry somewhere containing a cached list of the names of mounted volumes. This list would, naturally, include the name of TrueCrypt volumes, both standard and hidden. If the user gives a name to the hidden volume, it would appear in such a list. If an investigator were somehow able to determine that there were two TrueCrypt volume names but only one TrueCrypt device, the inference would be that there was a hidden volume. A good summary paper that also describes ways to infer the presence of hidden volumes — at least on some Windows systems — can be found in "Detecting Hidden Encrypted Volumes" (Hargreaves & Chivers).
Having nothing to do with TrueCrypt, but having something to do with plausible deniability and devious crypto schemes, is a new approach to holding password cracking at bay dubbed Honey Encryption. With most of today's crypto systems, decrypting with a wrong key produces digital gibberish while a correct key produces something recognizable, making it easy to know when a correct key has been found. Honey Encryption produces fake data that resembles real data for every key that is attempted, making it significantly harder for an attacker to determine whether they have the correct key or not; thus, if an attacker has a credit card file and tries thousands of keys to crack it, they will obtain thousands of possibly legitimate credit card numbers. See "'Honey Encryption' Will Bamboozle Attackers with Fake Secrets" (Simonite) for some general information or "Honey Encryption: Security Beyond the Brute-Force Bound" (Juels & Ristenpart) for a detailed paper.
5.12. Encrypting File System (EFS)
Microsoft introduced the Encrypting File System (EFS) with the NTFS v3.0 file system and has supported EFS since Windows 2000 and XP (although EFS was and is not supported in all variations of Windows). Since Windows 10, EFS can also be used on FAT and exFAT volumes. EFS can be used to encrypt individual files, directories, or entire volumes. While disabled by default, EFS encryption can be easily enabled via File Explorer (aka Windows Explorer) by right-clicking on the file, directory, or volume to be encrypted, selecting Properties, Advanced, and Encrypt contents to secure data (Figure 26). Note that encrypted files and directories are displayed in green in Windows Explorer.
FIGURE 26: EFS and Windows (File) Explorer. |
The Windows command prompt provides an easy tool with which to detect EFS-encrypted files on a disk. The cipher command has a number of options, but the /u/n switches can be used to list all encrypted files on a drive (Figure 27).
FIGURE 27: The cipher command. |
EFS supports a variety of secret key encryption schemes, including 3DES, DESX, AES, and ECC, as well as RSA public key encryption. The operation of EFS — at least at the theoretical level — is relatively straight-forward. When a file is saved to disk:
- A random File Encryption Key (FEK) is generated by the operating system.
- The file contents are encrypted using one of the SKC schemes and the FEK.
- The FEK is stored with the file, encrypted with the owner's RSA public key. In addition, the FEK is encrypted with the RSA public key of any other authorized users and, optionally, a recovery agent's RSA public key.
When the file is opened:
- The FEK is recovered using the RSA private key of the owner, other authorized user, or the recovery agent.
- The FEK is used to decrypt the file's contents.
There are weaknesses with the system, most of which are related to key management. As an example, the RSA private key can be stored on an external device such as a floppy disk (yes, really!), thumb drive, or smart card. In practice, however, this is rarely done; the user's private RSA key is often stored on the hard drive. In addition, early EFS implementations (prior to Windows XP SP2) tied the key to the username; later implementations employ the user's password.
A more serious implementation issue is that a backup file named esf0.tmp is created prior to a file being encrypted. After the encryption operation, the backup file is deleted — not wiped — leaving an unencrypted version of the file available to be undeleted. For this reason, it is best to use encrypted directories because the temporary backup file is protected by being in an encrypted directory.

FIGURE 28: EFS key storage. (Source: NTFS.com) |
The EFS information is stored as a named stream in the $LOGGED_UTILITY_STREAM Attribute (attribute type 256 [0x100]). This information includes (Figure 28):
- A Data Decryption Field (DDF) for each user authorized to decrypt the file, containing the user's Security Identifier (SID), the FEK encrypted with the user's RSA public key, and other information.
- A Data Recovery Field (DRF) with the encrypted FEK for every method of data recovery
Master File Table (MFT) Parser V2.1 - Gary C. Kessler (11 June 2013) : : 0056-0059 Attribute type: 0x10-00-00-00 [$STANDARD_INFORMATION] 0060-0063 Attribute length: 0x60-00-00-00 [96 bytes] 0064 Non-resident flag: 0x00 [Attribute is resident] : : 0152-0155 Attribute type: 0x30-00-00-00 [$FILE_NAME] 0156-0159 Attribute length: 0x70-00-00-00 [112 bytes] 0160 Non-resident flag: 0x00 [Attribute is resident] : : 0264-0267 Attribute type: 0x40-00-00-00 [$VOLUME_VERSION/$OBJECT_ID] 0268-0271 Attribute length: 0x28-00-00-00 [40 bytes] 0272 Non-resident flag: 0x00 [Attribute is resident] : : 0304-0307 Attribute type: 0x80-00-00-00 [$DATA] 0308-0311 Attribute length: 0x48-00-00-00 [72 bytes] 0312 Non-resident flag: 0x01 [Attribute is non-resident] 0313 Name length: 0x00 [0 16-bit characters] 0314-0315 Offset to name: 0x00-00 [0 bytes] 0316-0317 Flag: 0x00-40 -- Encrypted : : 0376-0379 Attribute type: 0x00-01-00-00 [$LOGGED_UTILITY_STREAM] 0380-0383 Attribute length: 0x50-00-00-00 [80 bytes] 0384 Non-resident flag: 0x01 [Attribute is non-resident] : 0440-0447 Name: 0x24-00-45-00-46-00-53-00 [$EFS] : : FIGURE 29: The $LOGGED_UTILITY_STREAM Attribute (see complete output at crypto_EFS.txt). |
Files in an NTFS file system maintain a number of attributes that contain the system metadata (e.g., the $STANDARD_INFORMATION attribute maintains the file timestamps and the $FILE_NAME attribute contains the file name). Files encrypted with EFS store the keys, as stated above, in a data stream named $EFS within the $LOGGED_UTILITY_STREAM attribute. Figure 29 shows the partial contents of the Master File Table (MFT) attributes for an EFS encrypted file.
5.13. Some of the Finer Details of RC4
RC4 is a variable key-sized stream cipher developed by Ron Rivest in 1987. RC4 works in output-feedback (OFB) mode, so that the key stream is independent of the plaintext. The algorithm is described in detail in Schneier's Applied Cryptography, 2/e, pp. 397-398 and the Wikipedia RC4 article.
RC4 employs an 8x8 substitution box (S-box). The S-box is initialized so that S[i] = i, for i=(0,255).
A permutation of the S-box is then performed as a function of the key. The K array is a 256-byte structure that holds the key (possibly supplemented by an Initialization Vector), repeating itself as necessary so as to be 256 bytes in length (obviously, a longer key results in less repetition). [[NOTE: All arithmetic below is assumed to be on a per-byte basis and so is implied to be modulo 256.]]
j = 0
for i = 0 to 255
j = j + S[i] + K[i]
swap (S[i], S[j])
Encryption and decryption are performed by XORing a byte of plaintext/ciphertext with a random byte from the S-box in order to produce the ciphertext/plaintext, as follows:
Initialize i and j to zero
For each byte of plaintext (or ciphertext):
i = i + 1
j = j + S[i]
swap (S[i], S[j])
z = S[i] + S[j]
Decryption: plaintext [i] = S[z] ⊕ ciphertext [i]
Encryption: ciphertext [i] = S[z] ⊕ plaintext [i]
A Perl implementation of RC4 (fine for academic, but not production, purposes) can be found at http://www.garykessler.net/software/index.html#RC4. This program is an implementation of the CipherSaber version of RC4, which employs an initialization vector (IV). The CipherSaber IV is a 10-byte sequence of random numbers between the value of 0-255. The IV is placed in the first 10-bytes of the encrypted file and is appended to the user-supplied key (which, in turn, can only be up to 246 bytes in length).
In 2014, Rivest and Schuldt developed a redesign of RC4 called Spritz. The main operation of Spritz is similar to the main operation of RC4, except that a new variable, w, is added:
i = i + w
j = k + S [j + S[i]]
k = i + k + S[j]
swap (S[i], S[j])
z = (S[j + S[i + S[z+k]]]
Decryption: plaintext [i] = S[z] ⊕ ciphertext [i]
Encryption: ciphertext [i] = S[z] ⊕ plaintext [i]
As seen above, RC4 has two pointers into the S-box, namely, i and j; Spritz adds a third pointer, k.
Pointer i move slowly through the S-box; note that it is incremented by 1 in RC4 and by a constant, w, in Spritz. Spritz allows w to take on any odd value, ensuring that it is always relatively prime to 256. (In essence, RC4 sets w to a value of 1.)
The other pointer(s) — j in RC4 or j and k in Spritz — move pseudorandomly through the S-box. Both ciphers have a single swap of entries in the S-box. Both also produce an output byte, z, as a function of the other parameters. Spritz, additionally, includes the previous value of z as part of the calculation of the new value of z.
5.14. Challenge-Handshake Authentication Protocol (CHAP)
CHAP, originally described in RFC 1994, and its variants (e.g., Microsoft's MS-CHAP) are authentication schemes that allow two parties to demonstrate knowledge of a shared secret without actually divulging that shared secret to a third party who might be eavesdropping.
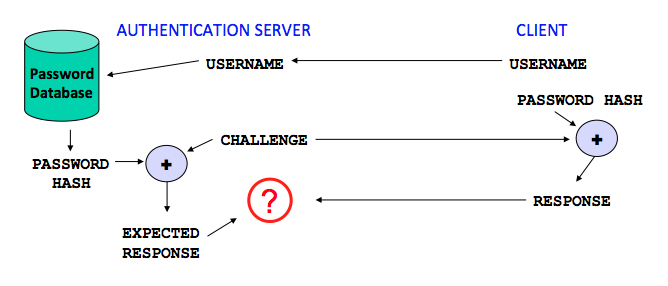
FIGURE 30: CHAP Handshake. |
The operation of CHAP is relatively straight-forward (Figure 30). Assume that the Client is logging on to a remote Server across the Internet. The Client needs to prove to the Server that it knows the password but doesn't want to reveal the password in any form that an eavesdropper can decrypt. In CHAP:
- The User sends their username (in plaintext) to the Server.
- The Server sends some random challenge string (i.e., some number of octets) to the User.
- The Server looks up the User's password in it's database and, using the same algorithm, generates an expected response string.
- The Server compares its expected response to the actual response sent by the User. If the two match, the User is authenticated.
Since the password is never revealed to a third-party, why can't we then just keep the same password forever? Note that CHAP is potentially vulnerable to a known plaintext attack; the challenge is plaintext and the response is encrypted using the password and a known CHAP algorithm. If an eavesdropper has enough challenge/response pairs, they might well be able to determine the password. Some other issues related to this form of authentication can be found in "Off-Path Hacking: The Illusion of Challenge-Response Authentication" (Gilad, Y., Herzberg, A., & Shulman, H., September-October 2014, IEEE Security & Privacy, 12(5), 68-77).
5.15. Secure E-mail and S/MIME
Electronic mail and messaging are the primary applications for which people use the Internet. Obviously, we want our e-mail to be secure; but, what exactly does that mean? And, how do we accomplish this task?
There are a variety of ways to implement or access secure e-mail and cryptography is an essential component to the security of electronic mail. And, the good news is that we have already described all of the essential elements in the sections above. From a practical perspective, secure e-mail means that once a sender sends an e-mail message, it can only be read by the intended recipient(s). That can only be accomplished if the encryption is end-to-end; i.e., the message must be encrypted before leaving the sender's computer and cannot be decrypted until it arrives at the recipient's system. But in addition to privacy, we also need the e-mail system to provide authentication, non-repudiation, and message integrity — all functions that are provided by a combination of hash functions, secret key crypto, and public key crypto. Secure e-mail services or software, then, usually provide two functions, namely, message signing and message encryption. Encryption, obviously, provides the secrecy; signing provides the rest.
Figure 4, above, shows how the three different types of crypto schemes work together. For purposes of e-mail, however, it is useful to independently examine the functions of signing and encryption, if for no other reason than while secure e-mail applications and services can certainly sign and encrypt a message, they may also have the ability to sign a message without encrypting it or encrypt a message without signing it.

FIGURE 31: Signing (top) and verifying (bottom) e-mail. (Source: https://technet.microsoft.com/en-us/library/aa995740(v=exchg.65).aspx) |
E-mail messages are signed for the purpose of authenticating the sender, providing a mechanism so that the sender cannot later disavow the message (i.e., non-repudiation), and proving message integrity — unless, of course, the sender claims that their key has been stolen. The steps of signing and verifying e-mail are shown in Figure 31. To sign a message:
- The sender's software examines the message body.
- Information about the sender is retrieved (e.g., the sender's private key).
- The signing operation (e.g., encrypting the hash of the message with the sender's private key) is performed.
- The Digital Signature is appended to the e-mail message.
- The signed e-mail message is sent.
Verification of the signed message requires the receiver's software to perform the opposite steps as the sender's software. In short, the receiver extracts the sender's Digital Signature, calculates a digital signature based upon the sender's information (e.g., using the sender's public key), and compares the computed signature with the received signature; if they match, the message's signature is verified. Note that if there are multiple recipients of the message, each will perform the same steps to verify the signature because the verification is based upon the sender's information (compare this to decryption, described below).

FIGURE 32: Encrypting (top) and decrypting (bottom) e-mail. (Source: https://technet.microsoft.com/en-us/library/aa995740(v=exchg.65).aspx) |
E-mail messages are encrypted for the purpose of privacy, secrecy, confidentiality — whatever term you wish to use to indicate that the message is supposed to be a secret between sender and receiver. The steps of encrypting and decrypting e-mail are shown in Figure 32. To encrypt a message:
- The sender's software examines the message body.
- The sender's software pulls out specific information about the recipient...
- ... and the encryption operation is performed.
- The encrypted message replaces the original plaintext e-mail message.
- The encrypted e-mail message is sent.
Note that if the message has multiple recipients, the encryption step will yield different results because the encryption step is dependent upon the recipient's information (e.g., their public key). One application might choose to send a different encrypted message to each recipient; another might send the same encrypted message to each recipient, but encrypt the decryption key differently for each recipient (note further that this latter approach might allow a recipient to perform a known plaintext attack against the other recipients; each recipient knows the decryption key for the message and also sees the key encrypted with the recipient's information). In any case, recipient-specific information (e.g., their private key) must be used in order to decrypt the message and the decryption steps performed by the recipient are essentially the opposite of those performed by the sender.
This discussion, so far, has been a little vague because different applications will act is different ways but, indeed, are performing very similar generic steps. There are two primary ways for a user to get send and receive secure e-mail, namely, to employ some sort of Web-based e-mail service or employ a secure e-mail client.
FIGURE 33: E-mail message to non-4SecureMail user. |
If the reader is interested in using a Web-based secure e-mail service, you have only to do an Internet search to find many such services. All have slightly different twists to them, but here are a few representative free and commercial options:
-
4SecureMail: Web-based e-mail service using 128-bit SSL between client and server; also supports many e-mail clients and mobile apps. Anonymous headers are "virtually untraceable." Non-4SecureMail recipients are notified by e-mail of waiting secure message which can be downloaded via browser; authenticity of the message is via the user's registered WaterMark (Figure 33).
-
CounterMail: Online, end-to-end e-mail service based upon OpenPGP. Multi-platform support, including Android. Has a USB key option, requiring use of a hardware dongle in order to retrieve mail.
-
Hushmail: Web- or client-based, end-to-end encrypted email based upon OpenPGP. Multi-platform support, including iPhone. Can send secure e-mail to non-Hushmail user by employing a shared password.
-
Kolab Now: Web-based secure e-mail service provider although it does not perform server-side e-mail encryption; they recommend that users employ a true end-to-end e-mail encryption solution. Data is stored on servers exclusively located in Switzerland and complies with the strict privacy laws of that country.
-
ProtonMail: End-to-end secure e-mail service using AES and OpenPGP, also located in Switzerland. Does not log users' IP addresses, thus provides an anonymous service. Multi-platform support, plus Android and iOS.
-
Tutanota: Web-, Android-, or iOS-based end-to-end secure e-mail service.
The alternative to using a Web-based solution is to employ a secure e-mail client or, at least, a client that supports secure e-mail. Using host-based client software ensures end-to-end security — as long as the mechanisms are used correctly. There are no lack of clients that support secure mechanisms; Apple Mail, Microsoft Outlook, and Mozilla Thunderbird, for example, all have native support for S/MIME and have plug-ins that support OpenPGP/GPG (see Section 5.5 for additional information on the signing and encryption capabilities of PGP).
The Secure Multipurpose Internet Mail Extensions (S/MIME) protocol is an IETF standard for use of public key-based encryption and signing of e-mail. S/MIME is actually a series of extensions to the MIME protocol, adding digital signature and encryption capability to MIME messages (which, in this context, refers to e-mail messages and attachments). S/MIME is based upon the original IETF MIME specifications and RSA's PKCS #7 secure message format, although it is now an IETF specification defined primarily in four RFCs:
- RFC 3369: Cryptographic Message Syntax (CMS) (based upon PKCS #7) — Describes the syntax (format) used to digitally sign, digest, authenticate, or encrypt any type of message content, the rules for encapsulation, and an architecture for certificate-based key management.
- RFC 3370: Cryptographic Message Syntax (CMS) Algorithms — Describes the use of common crypto algorithms to support the CMS, such as those for message digests (e.g., MD5 and SHA-1), signatures (e.g., DSA and RSA), key management, and content encryption (e.g., RC2 and 3DES).
- RFC 3850: Secure/Multipurpose Internet Mail Extensions (S/MIME) Version 3.1 Certificate Handling — Specifies how S/MIME agents use the Internet X.509 Public Key Infrastructure (PKIX) and X.509 certificates to send and receive secure MIME messages. (See Section 4.3 for additional information about X.509 certificates.)
- RFC 3851: Secure/Multipurpose Internet Mail Extensions (S/MIME) Version 3.1 Message Specification — Describes the "secure" part of the S/MIME protocol, add digital signature and encryption services to MIME. The MIME standard specifies the general structure for different content types within Internet messages; this RFC specifies cryptographically-enhanced MIME body parts.
A quite good overview of the protocol can be found in a Microsoft TechNet article titled "Understanding S/MIME."
Content-Type: multipart/signed; boundary="Apple-Mail=_6293E5DF-2993-4264-A32B-01DD43AB4259"; protocol="application/pkcs7-signature"; micalg=sha1 --Apple-Mail=_6293E5DF-2993-4264-A32B-01DD43AB4259 Content-Transfer-Encoding: 7bit Content-Type: text/plain; charset=us-ascii Hi Carol. What was that pithy Groucho Marx quote? /kess --Apple-Mail=_6293E5DF-2993-4264-A32B-01DD43AB4259 Content-Disposition: attachment; filename=smime.p7s Content-Type: application/pkcs7-signature; name=smime.p7s Content-Transfer-Encoding: base64 MIAGCSqGSIb3DQEHAqCAMIACAQExCzAJBgUrDgMCGgUAMIAGCSqGSIb3DQEHAQAAoIIJ9TCCBK8w ggOXoAMCAQICEQDgI8sVEoNTia1hbnpUZ2shMA0GCSqGSIb3DQEBCwUAMG8xCzAJBgNVBAYTAlNF MRQwEgYDVQQKEwtBZGRUcnVzdCBBQjEmMCQGA1UECxMdQWRkVHJ1c3QgRXh0ZXJuYWwgVFRQIE5l dHdvcmsxIjAgBgNVBAMTGUFkZFRydXN0IEV4dGVybmFsIENBIFJvb3QwHhcNMTQxMjIyMDAwMDAw WhcNMjAwNTMwMTA0ODM4WjCBmzELMAkGA1UEBhMCR0IxGzAZBgNVBAgTEkdyZWF0ZXIgTWFuY2hl c3RlcjEQMA4GA1UEBxMHU2FsZm9yZDEaMBgGA1UEChMRQ09NT0RPIENBIExpbWl0ZWQxQTA/BgNV BAMTOENPTU9ETyBTSEEtMjU2IENsaWVudCBBdXRoZW50aWNhdGlvbiBhbmQgU2VjdXJlIEVtYWls IENBMIIBIjANBgkqhkiG9w0BAQEFAAOCAQ8AMIIBCgKCAQEAibEN2npTGU5wUh28VqYGJre4SeCW 51Gr8fBaE0kVo7SMG2C8elFCp3mMpCLfF2FOkdV2IwoU00oCf7YdCYBupQQ92bq7Fv6hh6kuQ1JD FnyvMlDIpk9a6QjYz5MlnHuI6DBk5qT4VoD9KiQUMxeZrETlaYujRgZLwjPU6UCfBrCxrJNAubUI kzqcKlOjENs9IGE8VQOO2U52JQIhKfqjfHF2T+7hX4Hp+1SA28N7NVK3hN4iPSwwLTF/Wb1SN7Az aS1D6/rWpfGXd2dRjNnuJ+u8pQc4doykqTj/34z1A6xJvsr3c5k6DzKrnJU6Ez0ORjpXdGFQvsZA P8vk4p+iIQIDAQABo4IBFzCCARMwHwYDVR0jBBgwFoAUrb2YejS0Jvf6xCZU7wO94CTLVBowHQYD VR0OBBYEFJJha4LhoqCqT+xn8cKj97SAAMHsMA4GA1UdDwEB/wQEAwIBhjASBgNVHRMBAf8ECDAG AQH/AgEAMB0GA1UdJQQWMBQGCCsGAQUFBwMCBggrBgEFBQcDBDARBgNVHSAECjAIMAYGBFUdIAAw RAYDVR0fBD0wOzA5oDegNYYzaHR0cDovL2NybC51c2VydHJ1c3QuY29tL0FkZFRydXN0RXh0ZXJu YWxDQVJvb3QuY3JsMDUGCCsGAQUFBwEBBCkwJzAlBggrBgEFBQcwAYYZaHR0cDovL29jc3AudXNl cnRydXN0LmNvbTANBgkqhkiG9w0BAQsFAAOCAQEAGypurFXBOquIxdjtzVXzqmthK8AJECOZD8Vm am+x9bS1d14PAmEA330F/hKzpICAAPz7HVtqcgIKQbwFusFY1SbC6tVNhPv+gpjPWBvjImOcUvi7 BTarfVil3qs7Y+Xa1XPv7OD7e+Kj//BCI5zKto1NPuRLGAOyqC3U2LtCS5BphRDbpjc06HvgARCl nMo6x59PiDRuimXQGoq7qdzKyjbR9PzCZCk1r9axp3ER0gNDsY8+muyeMlP0dpLKhjQHuSzK5hxK 2JkNwYbikJL7WkJqIyEQ6WXH9dW7fuqMhSACYurROgcsWcWZM/I4ieW26RZ6H3kU9koQGib6fIr7 mzCCBT4wggQmoAMCAQICEQDvRS7kXtfrf7+LzZ7ZrvObMA0GCSqGSIb3DQEBCwUAMIGbMQswCQYD VQQGEwJHQjEbMBkGA1UECBMSR3JlYXRlciBNYW5jaGVzdGVyMRAwDgYDVQQHEwdTYWxmb3JkMRow GAYDVQQKExFDT01PRE8gQ0EgTGltaXRlZDFBMD8GA1UEAxM4Q09NT0RPIFNIQS0yNTYgQ2xpZW50 IEF1dGhlbnRpY2F0aW9uIGFuZCBTZWN1cmUgRW1haWwgQ0EwHhcNMTcwMTAxMDAwMDAwWhcNMTgw MTAxMjM1OTU5WjAkMSIwIAYJKoZIhvcNAQkBFhNnY2tAZ2FyeWtlc3NsZXIubmV0MIIBIjANBgkq hkiG9w0BAQEFAAOCAQ8AMIIBCgKCAQEA0ql2BQ6RbvG/9L4qGN7x9v3ieA5YFu0NKGF91J4ujNT5 upPhZl0K2u5Oa7Zj1WEf+1Jq+D7oj4px7C8nkJfJAyUVgZ9DfHysEliF4l4xSsVMwNUuAoWIYpfe iGKEL/X9U323yv2NNxkMTfiZ3WWsETNL43zzNwRGnu7hZmqpQsbNaIfhEXvC5BVZXv/B38jrq/v+ 6szdcvnjbhC+gkaaxNlj7xvJiVom0RESIqwwSkVNcn2KFu/Uja6NMzVApbkwwJfmTgEHm8jgiIEc +CHkeqkWF3u3HdE8a2xn8Xeg6IKlekZCtnEPwURF/IwWYq4BPdYKZIBkp9QQ5yr7KL4BVwIDAQAB o4IB8TCCAe0wHwYDVR0jBBgwFoAUkmFrguGioKpP7GfxwqP3tIAAwewwHQYDVR0OBBYEFJW+t4wQ BPSM0gdWl+x1+F76ThzAMA4GA1UdDwEB/wQEAwIFoDAMBgNVHRMBAf8EAjAAMCAGA1UdJQQZMBcG CCsGAQUFBwMEBgsrBgEEAbIxAQMFAjARBglghkgBhvhCAQEEBAMCBSAwRgYDVR0gBD8wPTA7Bgwr BgEEAbIxAQIBAQEwKzApBggrBgEFBQcCARYdaHR0cHM6Ly9zZWN1cmUuY29tb2RvLm5ldC9DUFMw XQYDVR0fBFYwVDBSoFCgToZMaHR0cDovL2NybC5jb21vZG9jYS5jb20vQ09NT0RPU0hBMjU2Q2xp ZW50QXV0aGVudGljYXRpb25hbmRTZWN1cmVFbWFpbENBLmNybDCBkAYIKwYBBQUHAQEEgYMwgYAw WAYIKwYBBQUHMAKGTGh0dHA6Ly9jcnQuY29tb2RvY2EuY29tL0NPTU9ET1NIQTI1NkNsaWVudEF1 dGhlbnRpY2F0aW9uYW5kU2VjdXJlRW1haWxDQS5jcnQwJAYIKwYBBQUHMAGGGGh0dHA6Ly9vY3Nw LmNvbW9kb2NhLmNvbTAeBgNVHREEFzAVgRNnY2tAZ2FyeWtlc3NsZXIubmV0MA0GCSqGSIb3DQEB CwUAA4IBAQAeZNE03prooHZKvzjDUbVFGfiX+pTPJxQjruFazJOK7iHd3PaadSlqBiyMJgazDBYY hvsjzrM0p9KV5z6pTyA8aWczvNTq+MgDymTPpCYOG6GSUHFIWok+iv/MVrJ/zhOgk81n9MuHe02t XYtg5r9UbEXpIOfhNt5ziMo9r37uHKl+kF+y5fF4YHyVcmlFGg0gzpOSdpvMdFWfpKm03jvpBITQ WDMrQ2vJs4vQUq0Qh+13cbOMc4cPHAAz+YXtcR2IiUPDDEfAPcgDSYfYeQlNHiGYVqWA9xGL9cDQ iyB1zp5TERWIfv2BnNdodupn+8LtoIX/cOJLyf16F8Lp1xBzMYIDxjCCA8ICAQEwgbEwgZsxCzAJ BgNVBAYTAkdCMRswGQYDVQQIExJHcmVhdGVyIE1hbmNoZXN0ZXIxEDAOBgNVBAcTB1NhbGZvcmQx GjAYBgNVBAoTEUNPTU9ETyBDQSBMaW1pdGVkMUEwPwYDVQQDEzhDT01PRE8gU0hBLTI1NiBDbGll bnQgQXV0aGVudGljYXRpb24gYW5kIFNlY3VyZSBFbWFpbCBDQQIRAO9FLuRe1+t/v4vNntmu85sw CQYFKw4DAhoFAKCCAekwGAYJKoZIhvcNAQkDMQsGCSqGSIb3DQEHATAcBgkqhkiG9w0BCQUxDxcN MTcwMTAxMTgwNDIwWjAjBgkqhkiG9w0BCQQxFgQUrhgwhfaU8cFbOsDvQEcl78xWH2wwgcIGCSsG AQQBgjcQBDGBtDCBsTCBmzELMAkGA1UEBhMCR0IxGzAZBgNVBAgTEkdyZWF0ZXIgTWFuY2hlc3Rl cjEQMA4GA1UEBxMHU2FsZm9yZDEaMBgGA1UEChMRQ09NT0RPIENBIExpbWl0ZWQxQTA/BgNVBAMT OENPTU9ETyBTSEEtMjU2IENsaWVudCBBdXRoZW50aWNhdGlvbiBhbmQgU2VjdXJlIEVtYWlsIENB AhEA70Uu5F7X63+/i82e2a7zmzCBxAYLKoZIhvcNAQkQAgsxgbSggbEwgZsxCzAJBgNVBAYTAkdC MRswGQYDVQQIExJHcmVhdGVyIE1hbmNoZXN0ZXIxEDAOBgNVBAcTB1NhbGZvcmQxGjAYBgNVBAoT EUNPTU9ETyBDQSBMaW1pdGVkMUEwPwYDVQQDEzhDT01PRE8gU0hBLTI1NiBDbGllbnQgQXV0aGVu dGljYXRpb24gYW5kIFNlY3VyZSBFbWFpbCBDQQIRAO9FLuRe1+t/v4vNntmu85swDQYJKoZIhvcN AQEBBQAEggEAi3e2rGbbeg0pkV1oaPVU/90jYkcqt3tYGNf5cDgySklQQARxuXhPpIroLLEKexrM m96Z5jB+c2Lo2LIZG9O7gFQkDF3wqU5YOB5m1PmTdQXaYjhttIKGAHHQs1vW0fhAXHIBRBI0d3j9 wK9svbxG7XwxDwZ9ED/tv4dbI9gyktbl6ppczAEC6+JoTGdLLPtEI9XgME9ZBh3ykXa87o46MgdQ FCTp5J2z1BMeP9B7FENvN9D+fi297HjCTFZoxKopoLQ92/Cud2w85+s6JbgeWlqAdNgAp4c24bxW Winw3N7LukDaWB1KdkfWKMsP2bJXF9uIDoPYTjvb2VO4kVEaBwAAAAAAAA== --Apple-Mail=_6293E5DF-2993-4264-A32B-01DD43AB4259-- FIGURE 34: Sample multipart/signed message. |
Figure 34 shows a sample signed message using S/MIME. The first few lines indicate that this is a multipart signed message using the PKCS #7 signature protocol and, in this case, the SHA-1 hash. The two text lines following the first --Apple-Mail=... indicates that the message is in plaintext; this is followed by the actual message. The next block indicates use of S/MIME where the signature block is in an attached file (the .p7s extension indicates that this is a signed-only message), encoded using BASE64.
Content-Type: application/pkcs7-mime; name=smime.p7m; smime-type=enveloped-data Content-Transfer-Encoding: base64 MIAGCSqGSIb3DQEHA6CAMIACAQAxggHOMIIBygIBADCBsTCBmzELMAkGA1UEBhMCR0IxGzAZBgNV BAgTEkdyZWF0ZXIgTWFuY2hlc3RlcjEQMA4GA1UEBxMHU2FsZm9yZDEaMBgGA1UEChMRQ09NT0RP IENBIExpbWl0ZWQxQTA/BgNVBAMTOENPTU9ETyBTSEEtMjU2IENsaWVudCBBdXRoZW50aWNhdGlv biBhbmQgU2VjdXJlIEVtYWlsIENBAhEA70Uu5F7X63+/i82e2a7zmzANBgkqhkiG9w0BAQEFAASC AQAbKAO7BoEKgZ9e/C837YpZYzspGdLbiMnRPmz3p2v+8H9DgPcOzMAjwdvT94el3hguke/Dn4LK L4/Un9ZbruoPzfps0Cxa8A+Acw2fVluYImKs0y3zCCOCQiKwW4IMWmS0HCvFTrHKGuGcWmpaFUv1 vTdFNPhQzF6jRJPv35GNtHWEFIRwqWFG1jOh/0uX0o3Cg8B1j/wwjTEkd0WU/DzYbe6nQSJzh7Kz 9guBAyfSVPZsLcvkd1ftP4vVrILnafKaFK9ls3al8dT5+oY7oTUHhem+oPMLcOnX0+ZZcqs97+oW HvQQy1lpofU8b/0Qt8lYZfAC5lMIOg6nMbmIUdjOMIAGCSqGSIb3DQEHATAUBggqhkiG9w0DBwQI hd7YXnfGNOeggAQYdIYlsYppSpTleDWPMbopt2Zu7+umGjuHBAiuLupldkuMbwQYorVXhHJ3J6G3 0Rad+eC3vbpu4Ohtcz/rBBAhZ97y8YgLhmSJzXCSLh5UBAisFO1grQ/WgQQIpwnzeRUrRikEMMo/ qTMXMBaFFmGRHgSbVaNTJOcpk11kmrZbUWUdSWUZwQ3TSdvnyVUJUUf7gFs8eQQop2w/yLoGZGVY DJFpaCBEbgBZAXbWeducGiDR8lUYOPdwjSnfb96yBgQIN2WZZMiZ6x4ECMQJ5uftbc+dBAj/LNyO TGk4awAAAAAAAAAAAAA= FIGURE 35: Sample S/MIME encrypted message. |
Figure 35 shows a sample encrypted message, carried as an S/MIME enveloped data attachment (.p7m) file, also formatted in BASE64. S/MIME can also attach certificate management messages (.p7c) and compressed data (.p7z). Many more S/MIME sample messages can be found in RFC 4134 ("Examples of S/MIME Messages").
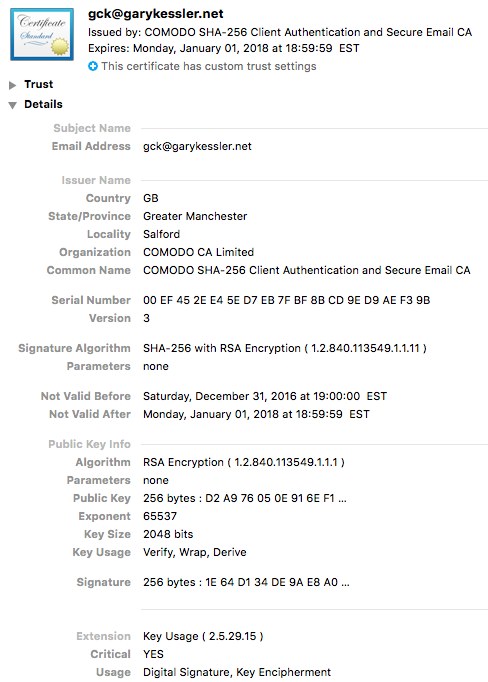
FIGURE 36: Sample S/MIME certificate. |
S/MIME is a powerful mechanism and is widely supported by many e-mail clients. To use your e-mail client's S/MIME functionality, you will need to have an S/MIME certificate (Figure 36). Several sites provide free S/MIME certificates for personal use, such as Instant SSL (Comodo), Secorio, and StartSSL (StartCom); commercial-grade S/MIME certificates are available from many other CAs. (NOTE: If these sites install your S/MIME certificate to your browser, you might need to export [backup] the certificate and import it so it can be seen by your e-mail application.)
Do note that S/MIME is not necessarily well-suited for use with Web-based e-mail services. First off, S/MIME is designed for true end-to-end (i.e., client-to-client) encryption and Web mail services provide server-to-server or server-to-client encryption. Second, while S/MIME functionality could be built into browsers, the end-to-end security offered by S/MIME requires that the private key be accessible only to the end-user and not to the Web server. Finally, end-to-end encryption makes it impossible for a third-party to scan e-mail for viruses and other malware, thus obviating one of the advantages of using a Web-based e-mail service in the first place.
5.16. Identity-Based Encryption (IBE)
Identity-Based Encryption is a public-key crypto scheme that can be used for key authentication by parties who do not have an a priori relationship. First proposed in 1984 by Adi Shamir, a sender can encrypt a message using the receiver's public key, which can be derived from an ASCII character string that represents some unique identifier of the receiver (e.g., an e-mail address, telephone number, or a ship's registry number).
IBE employs most of the concepts that we already know from other PKC schemes. First, every user has a private/public key pair, where the public key is widely distributed and the private key is a closely held secret. Second, while the keys in the key pair are mathematically related, a party that knows someone's public key cannot easily derive the matching private key. Finally, key distribution and management requires a trusted third-party — called the Private Key Generator (PKG) — but, unlike the certificate authority (CA) model, does not require an a priori relationship between the users and the PKG.
In an IBE system, the PKG generates its own master public/private key pair. The PKG can publish and distribute the Master Public Key, along with the algorithm used to derive keys; the PKG closely holds the Master Private Key as a secret. Any user in the IBE system can generate a public key using a unique identifying string (ID) in combination with the Master Public Key and the key-generation algorithm. In order to obtain a private key, the owner of the identifying string contacts the PKG which, in turn, derives the appropriate private key from the ID in combination with the Master Private Key.
By way of example, consider the case where Alice wants to send an encrypted message to Bob. Bob's email address, bobby@example.boats, is his unique ID string. Using the PKG's Master Public Key, Alice can derive Bob's public key from his ID string. With that, she can encrypt a message for Bob and send it to him. When Bob receives the message, he contacts the PKG and, using some mechanism specified by the PKG, authenticates himself as the true owner of the ID string. The PKG can then use Bob's ID string and the Master Private Key to derive his private key, which is then sent to Bob. At that point, Bob can decrypt Alice's message. Once Bob has his private key, of course, he can continue to use it for subsequent messages.
Using a similar but reverse process, Alice could use her own unique ID string (e.g., alice@example.wine) to obtain her private key from the PKG with which she could digitally sign the e-mail message that she sends to Bob. Bob would then use Alice's ID string to derive her public key in order to verify the signature.
In 2001, Dan Boneh from Stanford University and Matt Franklin from the University of California, Davis developed a practical implementation of IBE based on elliptic curves and a mathematical construct called the Weil Pairing. Clifford Cocks, from the U.K.'s Government Communications Headquarters (GCHQ), described another IBE solution based on quadratic residues in composite groups, also in 2001.
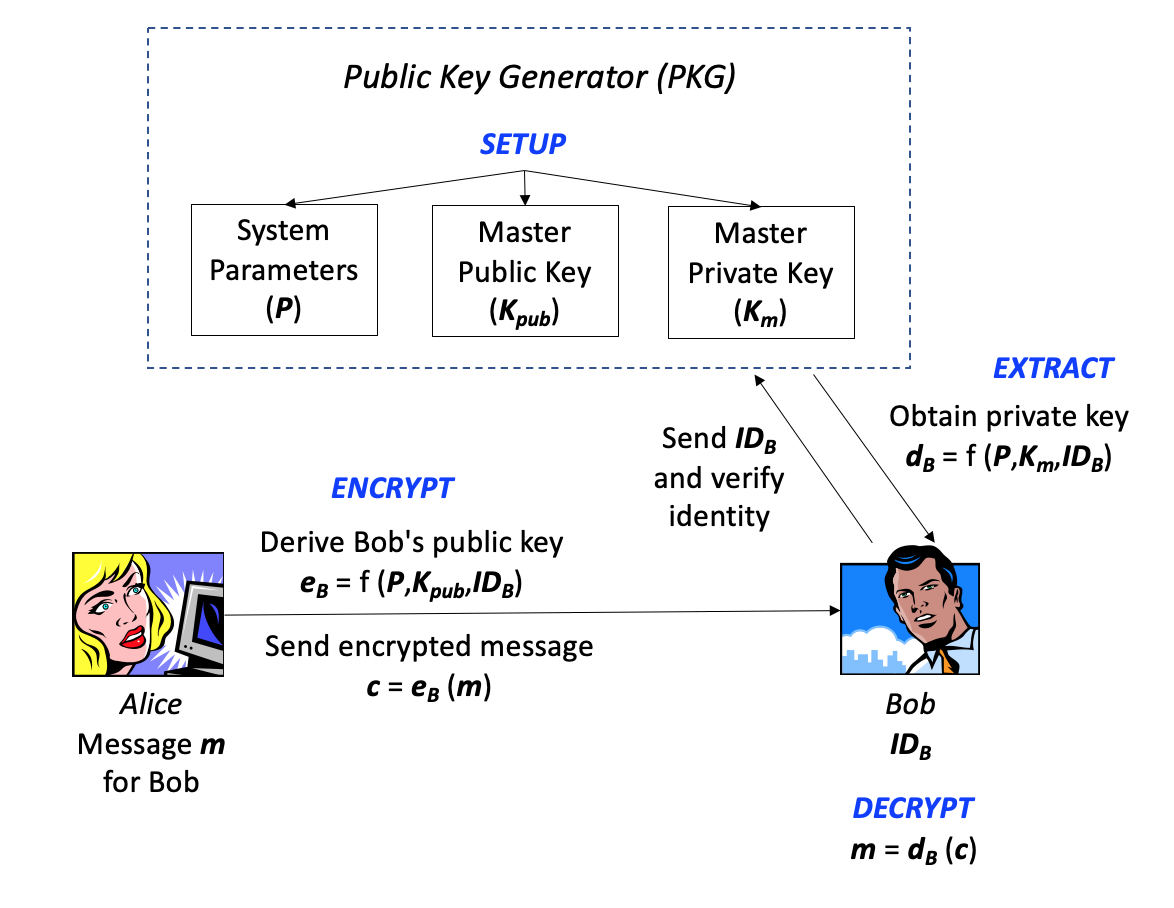
FIGURE 37: Identity-based encryption schema. |
Boneh and Franklin defined four basic functions that an IBE system needs to employ (Figure 37):
Setup: The setup algorithm is run once by the PKG to establish the IBE environment. This is the stage where the Master Public Key (Kpub) and Master Private Key (Km) are created. The Master Public Key and certain system parameters (P), such as the legal message space, legal ciphertext space, and key-derivation algorithm, can be shared widely, while Km is kept secret by the PKG.
Extract: When a user requests their private key, the PKG executes the extract algorithm. This is the step where the PKG verifies that the requesting party is the authentic owner of the ID string, although the specific method for doing this is actually outside the IBE protocol. The PKG uses the ID string to derive the user's private key (d) from the Master Private Key and sends it to the requesting party. In this example, Bob is requesting his private key and offers up his ID string, IDB. The PKG derives his private key, dB from the system parameters (P), the Master Private Key (Km), and Bob's ID string; this is shown in the figure as dB = f(P,Km,IDB). Alice would follow the same process to extract her private key.
Encrypt: In order for Alice to encrypt a message for Bob, she needs to obtain Bob's public key, eB, which can be derived from the system parameters (P), the Master Public Key (Kpub), and Bob's ID string. This is shown in the figure as eB = f(P,Kpub,IDB). Now armed with Bob's public key, Alice can encrypt the plaintext message (m) using Bob's public key; the output is the ciphertext string (c), shown in the figure as c = eB(m).
Decrypt: Bob decrypts the ciphertext string using his previously extracted private key, yielding the plaintext message. This is shown in the figure as m = dB(c).
The most practical IBE algorithms are based on elliptical curves, and include Boneh-Franklin (BF-IBE), Sakai-Kasahara (SK-IBE), and Boneh-Boyen (BB-IBE). Cocks' solution causes so much overhead (i.e., ciphertext expansion) as to be impractical expect for very short messages, such as key exchange for a secret key crypto scheme. (This is, ironically, where PKC schemes find themselves, in general; in the 1970s, PKC took up to three orders of magnitude more compute time than an SKC scheme to encrypt a message, thus the use of PKC for key exchange.) RFC 5091: Identity-Based Cryptography Standard (IBCS) #1 describes an implementation of IBE using Boneh-Franklin (BF) and Boneh-Boyen (BB1) Identity-based Encryption.
IBE has its pros and cons but is particularly useful in very dynamic environments where pre-distribution of public keys is not possible or not feasible. It requires, of course, that the PKG is highly trusted. The PKG is also a lucrative target for hackers because compromise of the PKG compromises every message sent by parties employing the system.
5.17. Shamir's Secret Sharing (SSS)
Shamir's Secret Sharing is a rather novel secret-sharing method where a group can work together to gain access to a resource. Adi Shamir, of RSA fame, described a method whereby a secret is divided into n parts in such a way that knowledge of any k parts allows the secret to be revealed; knowledge of any k-1 or fewer parts yields no information about the secret at all. This so-called (k,n) threshold scheme has many applications in real life. Consider this simple example from Shamir's original 1979 paper, "How to Share a Secret":
Consider ... a company that digitally signs all its checks... If each executive is given a copy of the company's secret signature key, the system is convenient but easy to misuse. If the cooperation of all the company's executives is necessary in order to sign each check, the system is safe but inconvenient. The standard solution requires at least three signatures per check, and it is easy to implement with a (3, n) threshold scheme. Each executive is given a small magnetic card with one Di piece, and the company's signature generating device accepts any three of them in order to generate (and later destroy) a temporary copy of the actual signature key D. The device does not contain any secret information and thus it need not be protected against inspection. An unfaithful executive must have at least two accomplices in order to forge the company's signature in this scheme.
The idea is conceptually straight-forward. Observe that a polynomial of degree k-1 is defined by k terms; e.g., the 2nd-degree polynomial 4x2+6x+15 has three terms. Suppose the secret, S, can be expressed as a number. We choose a prime number, P, so that S<P. A (k,n) threshold scheme requires 0<k≤n<P and is defined by the following polynomial of degree k-1:
f(x) = a0 + a1x + a2x2 + ... + ak-1xk-1
where a0=S and the remaining coefficients are random positive integers such that ai<P, for i=1...k-1.
We can now build a table of n values of the polynomial; i.e., f(i) for i = 1...n.
At this point, each of the n participants in the (k,n) scheme is given a different value of i in the range 1-n, as well as the corresponding integer output, f(i). If any subset of k participants puts their information together, they can reconstruct a polynomial of degree k-1 so that the a0 term takes on the value of the original secret, S. This is based on the fact that the system is designed so that the secret, divided into
So, here is a simple, but reasonably accurate, example of how SSS works. (It is simplified because it will employ integer arithmetic whereas the SSS scheme actually employs finite field arithmetic, resulting in a less than totally secure system; nevertheless, the reader should get the idea.) Let's build a (3,5) threshold system; i.e., one where the secret is split across five pieces and any three are required to reconstruct the secret. In this case, the secret, S, is represented by the number 18. We will choose 23 as the prime number P (which is larger than S, as required).
Since k=3, we need to create a polynomial of degree 2. This polynomial will need three coefficients; a0=S, and we will randomly choose a1=6 and a2=11 (as required, all values of a are smaller than P.) We now have the polynomial:
f(x) = 18 + 6x + 11x2
The next step is to create the table of the five outputs of the function, f(x), for all values x=1,...,5; each (x,f(x)) pair is denoted Tx:
T1 = (1,35)
T2 = (2,74)
T3 = (3,135)
T4 = (4,218)
T5 = (5,323)
Each of the five participants is provided with one of the T pairs. Now, let's see what happens when participants 1, 3, and 4, for example, get together to reconstruct the secret.
The SSS scheme relies on the fact that k points can be used to estimate the original n-part problem. For the reconstruction, we need to compute Lagrange polynomials — denoted L — which are used for polynomial interpolation. The Lagrange method finds the lowest degree polynomial that represents a function that coincides at a set of given points. In this example, we have three points: (x0,y0)=T1=(1,35), (x1,y1)=T3=(3,135), and (x2,y2)=T4=(4,218).
The formulas and solutions for the three Lagrange polynomials are:
The next step is to solve the Lagrange problem:
It turns out that the only coefficient that matters is the one for the x0 (ones) term, which is 18. This, of course, is the a0 coefficient which, by design, is the secret, S. This also points to a computational shortcut, namely, we can ignore any calculation involving any part of the polynomial other than the x0 term. Now, the calculation is merely:
f(x) = (35 ⋅ 2) + (135 ⋅ -2) + (218 ⋅ 1) = 18 = S
Shamir's original paper describes this pretty well and the Wikipedia page has a very detailed example.
5.18. Bit integrity, CRCs, and Hashes
Hash functions are used in crypto systems for message integrity, so that Bob can be ensured that the message he receives is the one that Alice sent. Hash functions do this by detecting bit errors in messages; even a single bit error in a large message will cause a significant change in the hash value. Hash functions, however, were not originally designed for message integrity; back in the early days of computer communications, longitudinal redundancy check (LRC) and cyclic redundancy check (CRC) algorithms, including the use of parity bits, were employed for bit error detection.
An LRC code is pretty trivial and operates on the bytes of the message. Generally, an LRC might merely take the exclusive-OR of all of the bytes in the message or compute the sum of all of the bytes, and append the checksum value to end of the message. While there are many variants of this, here are two examples. Suppose my message is the character string:
My name is Gary.
Using the ASCII character code, this message would appear in hexadecimal as 4D79206E616D6520697320476172792E. Taking the XOR of each byte would yield an LRC of 0x0A; summing the individual bytes (modulo 256) would yield a sum of 0x9C. When transmitting the message, the LRC bytes are appended to the end of the message. The receiver also calculates the LRC on the message and the receiver's value should match the transmitted value.
LRCs are very weak error detection mechanisms. If there is a single bit error, it will certainly be detected by an LRC. But an even number of errors in the same bit position within multiple bytes will escape detection by an XOR LRC. And a burst of errors might even escape detection by an additive LRC. The point is, it is trivial to create syndromes of bit errors that won't be found by an LRC code. (This is not to say that they are not used in some data transmission systems!)
CRCs were developed in the early 1960s to provide message integrity, bit-error detection, and, in some cases, bit-error correction in data communication systems. There are many CRC codes in use today, almost all in some sort of networking application. CRCs are expressed as an n-order polynomial yielding an n-bit result; i.e., a CRC-n polynomial is one with n+1 terms and is used to compute an n-bit checksum. An n-bit CRC code can be used with an arbitrary length input, can detect 100% of burst errors up to n bits in length, and can detect bursts of n bits or more with probability (1-2-n).
Common CRCs today yield checksums of 8, 16, 32, or 64 bits in length although other lengths are also used in some applications. Two example 16-bit CRCs are:
- CRC-16-ANSI: x16 + x15 + x2 + 1 (used in DECnet, Modbus, and USB)
- CRC-16-CCITT: x16 + x12 + x5 + 1 (used in Bluetooth, HDLC, and X.25)
If we take our message above, for example, the CRC-CCITT checksum value would be 0xBF9D.
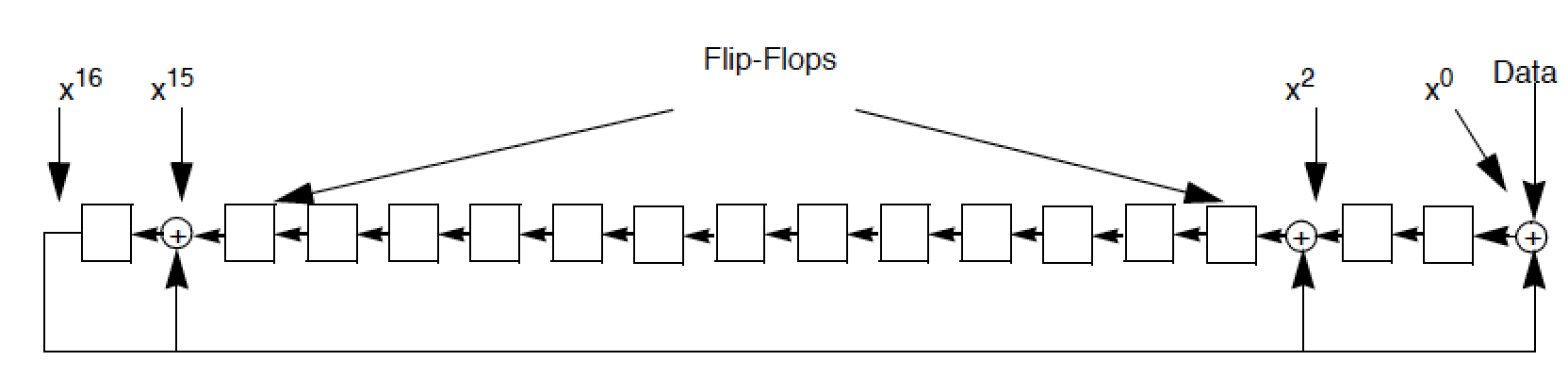
FIGURE 38: Hardware CRC-16-CCITT generator. (From Microchip AN730) |
CRCs are, in essence, a one-way stream cipher, receiving one bit of the message at a time, and using XOR gates and an n-bit shift register to compute the checksum. The contents of the register are the checksum value, where the register is generally initialized as all zeroes or all ones. This operation can be seen by looking at the hardware implementation of the CRC-16-CCITT checksum (Figure 38), taken from Microchip Application Note 730 (AN730).
Now, this stroll down memory lane (at least for me!) is really about why LRCs and CRCs are not used in cryptography. While they work fine for bit error detection and the fact that an arbitrary-length input produces a fixed-length output, they were not designed for the level of robustness required for cryptographic error detection and other functions. The origins of cryptographic hash functions (CHFs) date back to the early 1950s, when hash functions — aka, message digests — were used in computer science to map an arbitrary length data item to a bit array of fixed size; e.g., one application was to map variable-length variable names to a fixed-size token array for processing variables in a programming language's compiler or interpreter. It took another 20 years for hashing to be applied to cryptography.
Like a CRC, a CHF algorithm incorporated into a modern cryptosystem (say, starting in the late-1980s or early-1990s) can, theoretically, accept a message of arbitrary length and produce a fixed-length output. And, like CRCs, it is believed that it is computationally infeasible to produce two messages having the same message digest value or to produce a message having a given prespecified message digest value, given a strong message digest algorithm. Unlike CRCs, message digest algorithms are intended for digital signature applications; signing the "compressed" version of a message (i.e., the hash) is far more efficient than signing the entire message. Furthermore, signing the hash value takes the same amount of time regardless of the size of the message, thus making the time required for signing to be much more predictable than if signing an arbitrary length message. Also unlike CRCs, message digest algorithms have an encryption function integral to their computation.
Among the earliest of the hash algorithms incorporated into cryptosystems was Message Digest 5, described in 1992 in RFC 1321; the Secure Hash Algorithm came later, detailed in RFC 3174 in 2001. MD5 and SHA-1 produce a 128-bit and 160-bit output, respectively; MD5 accepts a message of arbitrary length while SHA-1 limits the input to 264-1 bits. The string above would generate the following hash values:
MD5 ("My name is Gary.") = 3b55c9c3503c456906b765fbaaf37223
SHA1 ("My name is Gary.") = e41d178d27d53066a7c87f5a422d74156a8c27b4
While hash algorithms are designed to be as simple as possible, they are much more complex than a CRC. So, here's a rundown on part of the MD5 calculation to give an idea of the manipulations. See the RFCs for sample code.
First off, MD5 operates on 128-bit blocks or, more precisely, four 32-bit words, at one time. Therefore, the initial step is to pad the incoming message so that it is an even multiple of 16 32-bit words (512 bits). The algorithm then steps through the input 128 bits at a time. I'll explain the process below and you'll see multiple passes over the data with a lot of transpositions and substitutions, which are the basic operations of encryption that were described earlier in this paper.
So, here is some basic MD5 terminology and nomenclature:
- The 128-bit block is divided into four 32-bit words. These values are stored in four registers, called A, B, C, and D. The MD5 specification provides the initial values of these registers prior to any calculation.
- MD5 defines four "auxiliary" functions — denoted F, G, H, and I — which are the guts of the transformation process. Each of these functions takes three 32-bit values (denoted x, y, and z below) as input and produces one 32-bit output. The functions are defined below in terms of the Boolean AND (•), OR (∨), XOR (⊕), and NOT (¬) functions (see this table of byte-based Boolean operations if you want to perform any of these operations by hand):
- F (x,y,z) = (x • y) ∨ (¬x • z)
- G (x,y,z) = (x • z) ∨ (y • ¬z)
- H (x,y,z) = x ⊕ y ⊕ z
- I (x,y,z) = y ⊕ (x ∨ ¬z)
- All of the arithmetic is performed modulo 232.
- One of the operations on the registers is called a circular shift, denoted by the "<<<" operator. The nomenclature "x <<< s" means to rotate (or circularly shift) the contents of the 32-bit x register by s bits to the left; bits that "fall off" on the left side of the register wrap around to the right side.
- There is a table of constants, denoted T, with 64 entries computed by applying the sine function to the values 1 to 64. (See the MD5 specification for details.)
- The 16-byte array, X, contains the 128-bit block that is being processed during a given round of operation.
The MD5 algorithm processes one 128-bit block as a time, sequentially stepping through the message. There is a feedback mechanism in place because all computations use the A, B, C, and D registers without zeroing them out between blocks. There are four rounds of processing on each 128-bit block, and each round comprises 16 operations. Each of the 64 operations uses the following generic formula:
a = b + ((a + f(b,c,d) + X[k] + T[i]) <<< s)
where:
- a, b, c, and d represent one of the 32-bit registers, A, B, C, or D, in the order specified below;
- f(b,c,d) represents one of the auxiliary functions, F, G, H, or I, as specified below, and using three 32-bit registers (b, c, and, d) as input;
- X[k] is the k-th byte (0-15) of the current 128-bit (16-byte) block, where k is specified below; and
- T[i] is the i-th entry (1-64) in the T table, where i is specified below.
The table below summarizes the characteristics of each operation within each round; remember that we start with operations 1-16 in round 1, then move on to round 2, etc.:
| Register Order |
ROUND 1 Function F | ROUND 2 Function G |
ROUND 3 Function H | ROUND 4 Function I | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Op. | k | i | s | Op. | k | i | s | Op. | k | i | s | Op. | k | i | s | |||||
| ABCD | 1 | 0 | 1 | 7 | 1 | 1 | 17 | 5 | 1 | 5 | 33 | 4 | 1 | 0 | 49 | 6 | ||||
| 2 | 4 | 5 | 2 | 5 | 21 | 2 | 1 | 37 | 2 | 12 | 53 | |||||||||
| 3 | 8 | 9 | 3 | 9 | 25 | 3 | 13 | 41 | 3 | 8 | 57 | |||||||||
| 4 | 12 | 13 | 4 | 13 | 29 | 4 | 9 | 45 | 4 | 4 | 61 | |||||||||
| DABC | 5 | 1 | 2 | 12 | 5 | 6 | 18 | 9 | 5 | 8 | 34 | 11 | 5 | 7 | 50 | 10 | ||||
| 6 | 5 | 6 | 6 | 10 | 22 | 6 | 4 | 38 | 6 | 3 | 54 | |||||||||
| 7 | 9 | 10 | 7 | 14 | 26 | 7 | 0 | 42 | 7 | 15 | 58 | |||||||||
| 8 | 13 | 14 | 8 | 2 | 30 | 8 | 12 | 46 | 8 | 11 | 62 | |||||||||
| CDAB | 9 | 2 | 3 | 17 | 9 | 11 | 19 | 14 | 9 | 11 | 35 | 16 | 9 | 14 | 51 | 15 | ||||
| 10 | 6 | 7 | 10 | 15 | 23 | 10 | 7 | 39 | 10 | 10 | 55 | |||||||||
| 11 | 10 | 11 | 11 | 3 | 27 | 11 | 3 | 43 | 11 | 6 | 59 | |||||||||
| 12 | 14 | 15 | 12 | 7 | 31 | 12 | 15 | 47 | 12 | 2 | 63 | |||||||||
| BCDA | 13 | 3 | 4 | 22 | 13 | 0 | 20 | 20 | 13 | 14 | 36 | 23 | 13 | 5 | 52 | 21 | ||||
| 14 | 7 | 8 | 14 | 4 | 24 | 14 | 10 | 40 | 14 | 1 | 56 | |||||||||
| 15 | 11 | 12 | 15 | 8 | 28 | 15 | 6 | 44 | 15 | 13 | 60 | |||||||||
| 16 | 15 | 16 | 16 | 12 | 32 | 16 | 2 | 48 | 16 | 9 | 64 | |||||||||
The way to interpret the information in the table is as follows. Remember, the generic formula for all operations is:
a = b + ((a + f(b,c,d) + X[k] + T[i]) <<< s)
So, if you want to understand, say, operation 11 in Round 3, the table says:
- The register order is CDAB, so a=C, b=D, c=A, and d=B
- Use function H, where registers D, A, and B will be the inputs (in that order)
- k = 3, i = 43, and s = 16
Given these values, the operation for this round would be computed as:
C = D + ((C + H(D,A,B) + X[3] + T[43]) <<< 16)
5.19. Keyed-Hash Message Authentication Code (HMAC)
IPsec authentication (for both AH and ESP), the Signal protocol, and many other communication schemes use HMAC, a Keyed-Hashing Message Authentication Code, to allow two users to mutually authenticate by demonstrating that they both know a secret without actually explicitly exchanging that secret. Described in FIPS PUB 198 and RFC 2104, HMAC uses a shared secret key between two parties rather than public key methods for message authentication. The advantage of this method of authentication is a simplicity in processing; PKC algorithms generally require three to five orders of magnitude (i.e., 1,000-100,000 times) more processing than an SKC scheme operating over the same message. If an application requires nothing more than authentication and needs fast processing, HMACs are an attractive alternative. The generic HMAC procedure can be used with just about any hash algorithm.
In HMAC, both parties share a secret key. The secret key will be employed with the hash algorithm in a way that provides mutual authentication without transmitting the key on the communications channel. Some key management procedure, external to the HMAC protocol, is used to manage key exchange between the two parties.
Recall that hash functions operate on fixed-size blocks of input at one time; MD5 and SHA-1, for example, work on 64-byte blocks. These functions then generate a fixed-size hash value; MD5 and SHA-1 produce 16-byte (128-bit) and 20-byte (160-bit) output strings, respectively. For use with HMAC, the secret key (K) should be at least as long as the hash output.
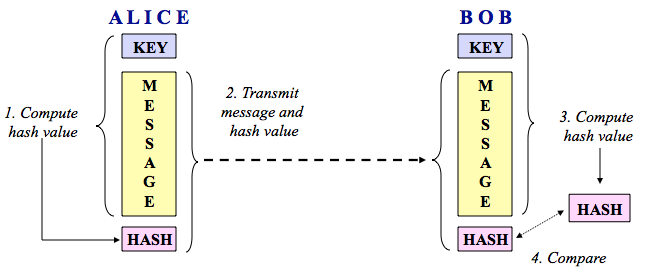
FIGURE 39: Keyed-hash MAC operation. |
The following steps provide a simplified, although reasonably accurate, description of how the HMAC scheme would work with a particular plaintext MESSAGE (Figure 39):
- Alice pads K so that it is as long as an input block; call this padded key Kp. Alice computes the hash of the padded key concatenated (.) with the message, i.e., HASH (Kp.MESSAGE).
- Alice transmits MESSAGE and the hash value.
- Bob has also padded K to create Kp. He computes HASH (Kp.MESSAGE) on the incoming message.
- Bob compares the computed hash value with the received hash value. If they match, then the sender — Alice — must know the secret key and her identity is, thus, authenticated.
HMACs are ideal for communication between two parties, say, Alice and Bob, who have a shared secret. They don't work as well in any sort of multicast environment, because all of the receivers — and there could be millions — would all have a single shared secret key. In a zero-trust environment, this greatly raises the opportunity for a rogue group member to send bogus messages. The common solution to this problem, of course, is to use a PKC methodology and employ a digital signature; Alice, for example, creates a signature with her private key and Bob, Carol, Dave, and all the other receivers can verify the signature using Alice's public key. In this case, none of the receivers who hold Alice's public key can spoof being Alice because they can't generate her signature. Indeed, the digital signature also provides the property of non-repudiation.
The problem with digital signatures is that they require a lot of computation for both sender and receiver(s); remember, PKC can require at least 1,000 times more processing for a given message compared to an SKC scheme. The resultant signature also reduces the bandwidth efficiency on a communications channel. So, digitally signing messages in a broadcast or large multicast environment where receivers want to authenticate each transmission is a challenge. (See the next section on TESLA for one possible solution.)
5.20. Timed Efficient Stream Loss-tolerant Authentication (TESLA)
The Timed Efficient Stream Loss-tolerant Authentication (TESLA) protocol, described in RFC 4082, provides a bandwidth-efficient, fault-tolerant mechanism so that a single key can be used for authentication by a large number of receivers in a multicast/broadcast environment. TESLA uses an HMAC-type scheme to provide time-delayed message authentication. The basic idea is that the sender uses a key for only a certain time interval (e.g., one second); during that time interval, receivers buffer all of the incoming messages. During the next time interval, the sender shares the previous interval's key with the receivers and starts to use a new key; receivers can now authenticate the buffered messages from the prior time interval even as they buffer new incoming messages.
TESLA requires the sender to generate a chain of authentication keys, where a given key is associated with a single time slot, T. In general, Ti+1 = Ti+Δt. The sender can create as many keys as it wants but might need to limit the length of the chain based upon memory or other constraints. So, suppose the sender wants to create a chain of N keys. The sender will randomly select the N-th (last) key in the chain, KN. Then, using a pseudo-random number generator (PRNG) function, P, and the last key value generated as the seed, the sender creates the prior key in the chain. Thus, KN-1 = P(KN), KN-2 = P(KN-1),..., K0 = P(K1). Each key is assigned to a time interval, so that Ki is associated with Ti. One important feature is that this is a one-way chain; given any key, Ki, all previously used keys can be derived by the receiver (i.e., any Kj can be calculated where j<i) but no following keys can be predicted (i.e., no Kj can be guessed where j>i).
The operation of TESLA is relatively straight-forward. During the T0 time slot, the sender employs an HMAC where K0 is the secret key. These messages are buffered by one or more receivers. When the T1 time slot starts, the sender sends K0 to the receiver(s) and starts to use K1 as the secret key. The receiver(s) can now authenticate the T0 buffered messages. Because of the properties of the one-way chain, the receiver(s) can derive keys from previous time slots that might have been lost due to transmission errors, thus providing fault tolerance.
For obvious reasons, TESLA requires loosely synchronized clocks between the sender and the receivers, but is not really intended for real-time services that cannot tolerate any delay. Check out the RFC or the paper by Perrig, Canetti, Tygar, and Song in RSA CryptoBytes for more detail. A light-weight version of the protocol, called µTESLA, was designed for sensor networks that have limited processing power, limited memory, and a real-time communication requirement. This version provides nearly immediate distribution of the authentication key and RC5 encryption. µTESLA is described in a paper by Perrig, Szewczyk, Tygar, Wen, and Culler in the ACM Journal of Wireless Networks.
6. QUANTUM CRYPTOGRAPHY
When this paper was originally prepared in the late-1990s, most crypto schemes were designed using basic integer arithmetic, logarithms and exponents, and prime number factorization, all for what today can only be described as classic computers. Resistance to brute-force attacks was provided by the expediency of using very large keys and requiring periodic changes to the key in order to "outrun" the available computing power necessary to try and guess every possible key value within the keyspace. Quantum computers, quantum algorithms, and quantum cryptography are changing the paradigms of modern and future cryptography. I am not an expert in this area so I am not going to talk about this subject in any great detail, but here is a quick intro and some pointers to additional information.
Today's computers employ a von Neumann architecture, based upon the design model introduced by Johnny von Neumann in the 1940s. Quantum computing requires an entirely new way of looking at computer hardware. The most fundamental difference between a classic computer and a quantum computer is the concept of a bit. In classic computers, a bit — aka binary digit — can take on only two values, namely, 0 or 1. A combination of two bits can take on four values — 00, 01, 10, and 11. To generalize, an n-bit string can take on 2n possible values, 0-(2n-1).
While classic computers define bits based upon storing data as electrical signals, quantum computers define storage based upon electrons and photons that can encode the data in multiple states. Due to a phenomenon known as superposition, a quantum bit, or qubit, can take on a state that is some combination of both 0 and 1 simultaneously; i.e., neither 0 nor 1, but something much more complicated. This means that two qubits can take on the four values mentioned above — 00, 01, 10, and 11 — at the same time! In theory, such a computer can solve problems too complex for conventional computers.
 FIGURE 40: Classical computing bit and quantum computing qubit. (Strathclyde University) |
There are many sources of information about quantum computing online and in various journal papers and articles. Here are a few places where you can start:
- Quantum Computing page at University of Strathclyde
- Quantum Computing page at Wikipedia
- Kietzmann, J., Demetis, D.S., Eriksson, T., & Dabirian, A. (2021, July-August). Hello Quantum! How Quantum Computing Will Change the World. IT Professional, 23(4), 106-111. DOI: 10.1109/MITP.2021.3086917
- Middleton , C. (2021, March 5). What's Under the Hood of a Quantum Computer? Physics Today. DOI: 10.1063/PT.6.1.20210305a
In theory, a quantum computer can solve problems that are too computationally complex for a today's conventional computers. The implications for employing quantum methods to attack classic cryptography algorithms should be readily apparent. Since we can theoretically build a computer where an n-qubit device can take on 2n states at the same time, it renders an n-bit keyspace susceptible to a nearly immediate brute-force attack. Before any panic sets in, recognize that quantum computers today are relatively small, so a large keyspace (say, 256 bits or larger) is as safe today from a quantum computer brute-force attack as a smaller key (e.g., 128 bits or smaller) is against a brute-force attack from a classic computer. Clearly, there will be this battle for some time keeping the key size large enough to withstand quantum attacks. (This is similar to the increasing size of RSA keys to keep them computationally infeasible to factor.) Meanwhile, a functional quantum computer that can pose a serious attack on cryptographic schemes as we know them today does not exist, and won't for many years — if ever. That said, it would be folly to ignore the potential threat and be blindsided.
Intertestingly, symmetric cryptography is generally considered quantum-safe. Grover's algorithm is the only known quantum attack against symmetric key cryptography and, aside from this, there are no quantum algorithms to crack secret keys. Thus, many PKC schemes are at greater risk than SKC schemes. Most PKC schemes — including RSA — use some form of prime factorization. Even though PKC schemes typically use keys that are an order of magnitude larger than those of SKC methods, the prime factorization algorithms are susceptible to attack using Shor's algorithm, a quantum computing method for finding the prime factors of an integer.
The classic method to determine the prime factors of an integer is called the general number field sieve. The time required to factor an integer, N, with the field sieve algorithm rises exponentially, increasing as a function of elog N. (Euler's Number — known as e — is an irrational number with a value 2.7182818284590452353....) Shor's algorithm, developed by Peter Shor in 1994, can solve the problem in polynomial time, or a value that is a function of log N.
NOTE: Here's a quick word on e and the log function. First, a review of logarithms. A base x logarithmic value of a number is the power of x that equals the number. So, for example, the log function with no subscript implies a base of 10. Therefore, log 100 = 2 because 102=100, and log 1000 = 3. Similarly, log2 1024 = 10 because 210=1024 and log2 65,536 = 16. Note that when we say that some set of values increases exponentially, we mean that they rise as a power of some base, rather than linearly as the multiple of some base. The value e (2.718281828459045...) is the basis for natural logarithms and many applications in mathematics; a natural logarithm is merely loge (denoted ln). The exponentiation function applied to a number is the inverse of determining the logarithm of a number.
x ex log x elog x 0 1 undefined undefined 1 2.7182818... 0 1 10 ≈22026 1 2.7182818... 100 ≈2.688117x1043 2 7.3890561... 1000 ≈1.970071x10434 3 20.0855369...
So, back to the compute time comparison between the general number field sieve and Shor's algorithm. As the table above shows, powers of e grow quite rapidly while logarithms increase slowly. This has a clear impact on computational complexity. Problems that grow exponentially in terms of complexity eventually rise to a level such that no computer can actually provide a solution, even though the algorithm is known. Quantum computers can reduce the complexity of some of these problems so that they become computationally feasible. In terms of cryptography, if a quantum computer with a sufficient number of qubits could operate without succumbing to some of the problems of quantum computing (e.g., quantum noise and other quantum-decoherence phenomena), then Shor's algorithm could be used to break PKC schemes such as RSA, Diffie-Hellman key exchange, and Elliptic Curve Diffie-Hellman key exchange. It won't affect SKC schemes, such as AES, that are not based on prime factorization.
Again, there's a ton more that you can read about this topic; here are some starting points:
- Quantum Cryptography page at Wikipedia
- Shor's Algorithm page at Wikipedia
- Bogomolec, X., Underhill, J.G., & Kovac, S.A. (2019). Towards Post-Quantum Secure Symmetric Cryptography: A Mathematical Perspective. Cryptology ePrint Archive, Paper 2019/1208.
- Hamdi, S.H., Zuhori, S.T., Mahmud, F., & Pal, B. (2014). A Compare Between Shor's Quantum Factoring Algorithm and General Number Field Sieve. In Proceedings of the 2014 International Conference on Electrical Engineering and Information & Communication Technology, April 10-12, 2014, pp. 1-6. DOI: 10.1109/ICEEICT.2014.6919115
- Schneier, B. (2018, September/October). Cryptography After the Aliens Land. IEEE Security and Privacy, 16(5), 86-88. DOI: 10.1109/MSP.2018.3761724 or https://www.schneier.com/essays/archives/2018/09/cryptography_after_t.html
Let the games begin!!! Bruce Schneier reports, in a January 2023 blog titled " Breaking RSA with a Quantum Computer," that a group of Chinese researchers claim to have a quantum computer design that can break 2048-bit RSA. It's an interesting read about what they claim what they can do versus what is actually possible. And then there are a number of updates to the blog with responses by others saying that the claim is false. We're going to see a lot of this for the next few years.
Meanwhile, a team of Chinese researchers, led by Shanghai University, has demonstrated that D-Wave's quantum annealing computers can crack RSA, AES, and other similar encryption methods. The report was published in the Chinese Journal of Computers, 47(5), May 2024.
In 2019, researchers at the Google AI Quantum team published this in the abstract to a paper: "The promise of quantum computers is that certain computational tasks might be executed exponentially faster on a quantum processor than on a classical processor. A fundamental challenge is to build a high-fidelity processor capable of running quantum algorithms in an exponentially large computational space. Here we report the use of a processor with programmable superconducting qubits to create quantum states on 53 qubits, corresponding to a computational state-space of dimension 253 (about 1016)." (See: Arute, F., Arya, K., Babbush, R. et al. Quantum supremacy using a programmable superconducting processor. Nature 574, 505-510 (2019). DOI: https://doi.org/10.1038/s41586-019-1666-5.) But quantum computers have, historically, had logical error rates that were too high to make the quantum computers practical. Maybe... until now? See: Google Quantum AI and Collaborators. Quantum error correction below the surface code threshold. Nature (2024, December 9). DOI: https://doi.org/10.1038/s41586-024-08449-y.
The paragraphs above are preamble to an introduction to NIST's post-quantum cryptographic standard (PQCS). In 2016, NIST started a competition to replace current PKC and digital signature algorithms with quantum-resistant cryptography, new methods that include "cryptographic algorithms or methods that are assessed not to be specifically vulnerable to attack by either a CRQC [cryptanalytically relevant quantum computer] or classical computer" (Prepare for a New Cryptographic Standard to Protect Against Future Quantum-Based Threats, July 5, 2022).
NIST has successfully used open competitions in the past, resulting in a new SKC standard (AES) in 2001 and a new hash function standard (SHA-3) in 2015. NIST received 82 PWCS proposals from around the world in 2017; 69 submissions made it through the Round 1 review, although five were subsequently withdrawn. In 2019, 26 submissions, including 17 public-key encryption and key-establishment Algorithms, and 9 digital signature algorithms, were announced as Round 2 finalists. Seven of the algorithms, including four public-key encryption and key-establishment algorithms, and three digital signature algorithms (plus eight alternate candidates) became Round 3 finalists in 2020. Finally, four public-key encryption and key-establishment algorithms — BIKE, Classic McEliece, HQC, and SIKE — became Round 4 finalists in July 2022.
Although the competition has been going on for several years, new cryptanalytic methods have been discovered that can be used against classic and post-quantum algorithms, and new weaknesses are being found in late-round algorithms.
- One Round X algorithm, Rainbow, was found to be so broken that it could be cracked with an off-the-shelf laptop in about two days.
- Three Round X finalists (Kyber, Saber, and Dilithium) were attacked with new methods that will likely be able to be employed against other PQCS algorithms.
- In August 2022, Round 4 finalist SIKE was successfully attacked in one hour by a single-core PC, using a classic (rather than quantum-specific) attack.
So, the process continues and the future will be one of determining the viability of building quantum computers and the ability to build quantum cryptographic algorithms. As usual, a massive amount of information can be found in the Web, here are some places to start looking:
- Post-Quantum Cryptography Standardization page at NIST
- Cybersecurity and Infrastructure Security Agency (CISA). (2022, July 5). Prepare for a New Cryptographic Standard to Protect Against Future Quantum-Based Threats. https://www.cisa.gov/uscert/ncas/current-activity/2022/07/05/prepare-new-cryptographic-standard-protect-against-future-quantum
- Goodin, D. (2022, August). Post-Quantum Encryption Contender is Taken out by Single-Core PC and 1 Hour. ARS Technica. https://arstechnica.com/information-technology/2022/08/sike-once-a-post-quantum-encryption-contender-is-koed-in-nist-smackdown/
- Schneier, B. (2022, August). NIST’s Post-Quantum Cryptography Standards Competition. Schneier on Security blog. https://www.schneier.com/blog/archives/2022/08/nists-post-quantum-cryptography-standards.html
In August 2024, NIST released three encryption tools designed to withstand attack by a quantum computer. These post-quantum encryption standards are designed to be general-purpose, securing everything from e-mail to e-commerce. These new standards are:
- Module-Lattice-Based Key-Encapsulation Mechanism Standard (FIPS 203)
- Module-Lattice-Based Signature Standard (FIPS 204)
- Stateless Standard Hash-Based Digital Signature (FIPS 205)
A large number of luminaries in the crypto community are cautious in their optimism of the impact of quantum cryptography, and even on the need for PQCS. Peter Gutman has an excellent 2024 presentation titled "Why Quantum Cryptanalysis is Bollocks," which is a good read on the topic. In the paper "Replication of Quantum Factorisation Records with an 8-bit Home Computer, an Abacus, and a Dog" (March 2025), Gutmann and Stephan Neuhaus note that IBM implemented Shor's algorithm in a seven-qubit quantum computer in 2001, demonstrating the factorization of the number 15. A decade later, researchers managed to use a quantum computer to factor the number 21. IBM tried to factor 35 in 2019 but basically failed — the algorithm worked only 14 percent of the time due to rampant qubit errors.
As notd above, researchers affiliated with Shanghai University claim to have used a quantum computer from D-Wave, which specializes in quantum annealing computers tuned for specific optimization problems, to have factored a 2,048-bit RSA integer. According to Gutmann and Neuhaus, however, the RSA number evaluated was the product of two prime factors that were too close together.
See also "Quantum code breaking? You'd get further with an 8-bit computer, an abacus, and a dog" for some additional information on this critique.
7. CONCLUSION AND SOAP BOX
This paper has briefly (well, it started out as "briefly"!) described how digital cryptography works. The reader must beware, however, that there are a number of ways to attack every one of these systems; cryptanalysis and attacks on cryptosystems, however, are well beyond the scope of this paper. In the words of Sherlock Holmes (ok, Arthur Conan Doyle, really), "What one man can invent, another can discover" ("The Adventure of the Dancing Men," in: The Return of Sherlock Holmes, 1903).
There are a lot of topics that have been discussed above that will be big issues going forward in cryptography. As compute power increases, attackers can go after bigger keys and local devices can process more complex algorithms. Some of these issues include the size of public keys, the ability to forge public key certificates, which hash function(s) to use, and the trust that we will have in random number generators. Interested readers should check out "Recent Parables in Cryptography" (Orman, H., January/February 2014, IEEE Internet Computing, 18(1), 82-86).
Cryptography is a particularly interesting field because of the amount of work that is, by necessity, done in secret. The irony is that secrecy is not the key (no pun intended) to the goodness of a cryptographic algorithm. Regardless of the mathematical theory behind an algorithm, the best algorithms are those that are well-known and well-documented because they are also well-tested and well-studied! In fact, time is the only true test of good cryptography; any cryptographic scheme that stays in use year after year is most likely a good one. The strength of cryptography lies in the choice (and management) of the keys; longer keys will resist attack better than shorter keys.
The corollary to this is that consumers should run, not walk, away from any product that uses a proprietary cryptography scheme, ostensibly because the algorithm's secrecy is an advantage. The observation that a cryptosystem should be secure even if everything about the system — except the key — is known by your adversary has been a fundamental tenet of cryptography for well over 125 years. It was first stated by Dutch linguist Auguste Kerckhoffs von Nieuwenhoff in his 1883 (yes, 1883) papers titled La Cryptographie militaire, and has therefore become known as "Kerckhoffs' Principle."
SIDEBAR: Getting a new crypto scheme accepted, marketed, and, commercially viable is a hard problem particularly if someone wants to make money off of the invention of a "new, unbreakable" methodology. Many people want to sell their new algorithm and, therefore, don't want to expose the scheme to the public for fear that their idea will be stolen. I observe that, consistent with Kerckhoffs' Principle, this approach is doomed to fail. A company won't invest in a secret scheme because there's no need; one has to demonstrate that their algorithm is better and stronger than what is currently available before someone else will invest time and money to explore an unknown promise. Regardless, I would also suggest that the way to make money in crypto is in the packaging — how does the algorithm fit into user applications and how easy is it for users to use? Check out a wonderful paper about crypto usability, titled "Why Johnny Can't Encrypt" (Whitten, A., & Tygar, J.D., 1999, Proceedings of the 8th USENIX Security Symposium, August 23-26, 1999, Washington, D.C., pp. 169-184.).
As a slight aside, another way that people try to prove that their new crypto scheme is a good one without revealing the mathematics behind it is to provide a public challenge where the author encrypts a message and promises to pay a sum of money to the first person — if any — who cracks the message. Ostensibly, if the message is not decoded, then the algorithm must be unbreakable. As an example, back in ~2011, a $10,000 challenge page for a new crypto scheme called DioCipher was posted and scheduled to expire on 1 January 2013 — which it did. That was the last that I heard of DioCipher. I leave it to the reader to consider the validity and usefulness of the public challenge process.
Finally, I can't ignore crypto snake oil or, to be fair, things that appear to be snake oil. The saga of Crown Sterling, a self-proclaimed "leading digital cryptography firm," is a case in point. Crown Sterling revealed a scheme called TIME AI™ — "the World's First 'Non-factor' Based Quantum Encryption Technology" — at BlackHat 2019. Sounds pretty cool but even a shallow analysis shows a lot of use of buzzwords, hand-waving, and excellent graphics... but no math, no algorithms, and no code. There's been a lot written about this and it is a good case study for the student of cryptography; for a short list, see:
- Gallagher, S. (2019, September 20). Medicine show: Crown Sterling demos 256-bit RSA key-cracking at private event. Ars Technica. https://arstechnica.com/information-technology/2019/09/medicine-show-crown-sterling-demos-256-bit-rsa-key-cracking-at-private-event/
- Schneier, B. (2019, September 5). The Doghouse: Crown Sterling. Schneier on Security. https://www.schneier.com/blog/archives/2019/09/the_doghouse_cr_1.html
- Schneier, B. (2019, September 20). Crown Sterling Claims to Factor RSA Keylengths First Factored Twenty Years Ago. Schneier on Security. https://www.schneier.com/blog/archives/2019/09/crown_sterling_.html
- Without Bullshit. (2019, August 13). Is this Crown Sterling press release from another planet? https://withoutbullshit.com/blog/is-this-crown-sterling-press-release-from-another-planet
8. REFERENCES AND FURTHER READING
- Bamford, J. (1983). The Puzzle Palace: Inside the National Security Agency, America's most secret intelligence organization. New York: Penguin Books.
- Bamford, J. (2001). Body of Secrets : Anatomy of the Ultra-Secret National Security Agency from the Cold War Through the Dawn of a New Century. New York: Doubleday.
- Barr, T.H. (2002). Invitation to Cryptology. Upper Saddle River, NJ: Prentice Hall.
- Basin, D., Cremers, C., Miyazaki, K., Radomirovic, S., & Watanabe, D. (2015, May/June). Improving the Security of Cryptographic Protocol Standards. IEEE Security & Privacy, 13(3), 24:31.
- Bauer, F.L. (2002). Decrypted Secrets: Methods and Maxims of Cryptology, 2nd ed. New York: Springer Verlag.
- Belfield, R. (2007). The Six Unsolved Ciphers: Inside the Mysterious Codes That Have Confounded the World's Greatest Cryptographers. Berkeley, CA: Ulysses Press.
- Boneh, D., & Shoup, V. (2020, January). A Graduate Course in Applied Cryptography, v0.5. https://toc.cryptobook.us/book.pdf.
- Denning, D.E. (1982). Cryptography and Data Security. Reading, MA: Addison-Wesley.
- Diffie, W., & Landau, S. (1998). Privacy on the Line. Boston: MIT Press.
- Electronic Frontier Foundation. (1998). Cracking DES: Secrets of Encryption Research, Wiretap Politics & Chip Design. Sebastopol, CA: O'Reilly & Associates.
- Esslinger, B., & the CrypTool Team. (2017, January 21). The CrypTool Book: Learning and Experiencing Cryptography with CrypTool and SageMath, 12th ed. CrypTool Project. https://www.cryptool.org/images/ctp/documents/CT-Book-en.pdf
- Federal Information Processing Standards (FIPS) 140-2. (2001, May 25). Security Requirements for Cryptographic Modules. Gaithersburg, MD: National Institute of Standards and Technology (NIST). http://csrc.nist.gov/publications/fips/fips140-2/fips1402.pdf
- Ferguson, N., & Schneier, B. (2003). Practical Cryptography. New York: John Wiley & Sons.
- Ferguson, N., Schneier, B., & Kohno, T. (2010). Cryptography Engineering: Design Principles and Practical Applications. New York: John Wiley & Sons.
- Flannery, S. with Flannery, D. (2001). In Code: A Mathematical Journey. New York: Workman Publishing Company.
- Ford, W., & Baum, M.S. (2001). Secure Electronic Commerce: Building the Infrastructure for Digital Signatures and Encryption, 2nd ed. Englewood Cliffs, NJ: Prentice Hall.
- Garfinkel, S. (1995). PGP: Pretty Good Privacy. Sebastopol, CA: O'Reilly & Associates.
- Grant, G.L. (1997). Understanding Digital Signatures: Establishing Trust over the Internet and Other Networks. New York: Computing McGraw-Hill.
- Grabbe, J.O. (1997, October 10). Cryptography and Number Theory for Digital Cash. http://www-swiss.ai.mit.edu/6.805/articles/money/cryptnum.htm
- Haufler, H. (2003). Codebreakers' Victory: How the Allied Cryptographers Won World War II. New York: Open Road Integrated Media.
- Kahn, D. (1983). Kahn on Codes: Secrets of the New Cryptology. New York: Macmillan.
- Kahn, D. (1996). The Codebreakers: The Comprehensive History of Secret Communication from Ancient Times to the Internet, revised ed. New York: Scribner.
- Katz, J., & Lindell, Y. (2021). Introduction to Modern Cryptography. Boca Raton, FL: Chapman & Hall/CRC Press, Taylor & Francis Group.
- Kaufman, C., Perlman, R., & Speciner, M. (1995). Network Security: Private Communication in a Public World. Englewood Cliffs, NJ): Prentice Hall.
- Koblitz, N. (1994). A Course in Number Theory and Cryptography, 2nd ed. New York: Springer-Verlag.
- Levy, S. (1999, April). The Open Secret. WIRED Magazine, 7(4). http://www.wired.com/wired/archive/7.04/crypto.html
- Levy, S. (2001). Crypto: How the Code Rebels Beat the Government — Saving Privacy in the Digital Age. New York: Viking Press.
- Mao, W. (2004). Modern Cryptography: Theory & Practice. Upper Saddle River, NJ: Prentice Hall Professional Technical Reference.
- Marks, L. (1998). Between Silk and Cyanide: A Codemaker's War, 1941-1945. New York: The Free Press (Simon & Schuster).
- National Academies of Sciences, Engineering, and Medicine. (2022). Cryptography and the Intelligence Community: The Future of Encryption. Washington, DC: The National Academies Press. DOI: 10.17226/26168.
- Schneier, B. (1996). Applied Cryptography, 2nd ed. New York: John Wiley & Sons.
- Schneier, B. (2000). Secrets & Lies: Digital Security in a Networked World. New York: John Wiley & Sons.
- Simion, E. (2015, January/February). The Relevance of Statistical Tests in Cryptography. IEEE Security & Privacy, 13(1), 66:70.
- Singh, S. (1999). The Code Book: The Evolution of Secrecy from Mary Queen of Scots to Quantum Cryptography. New York: Doubleday.
- Smart, N. (2014). Cryptography: An Introduction, 3rd ed. https://www.cs.umd.edu/~waa/414-F11/IntroToCrypto.pdf
- Smith, L.D. (1943). Cryptography: The Science of Secret Writing. New York: Dover Publications.
- Spillman, R.J. (2005). Classical and Contemporary Cryptology. Upper Saddle River, NJ: Pearson Prentice-Hall.
- Stallings, W. (2006). Cryptography and Network Security: Principles and Practice, 4th ed. Englewood Cliffs, NJ: Prentice Hall.
- Young, A., & Yung, M. (2004). Malicious Cryptography: Exposing Cryptovirology. New York: John Wiley & Sons.
- On the Web:
- Bob Lord's Online Crypto Museum
- Crypto Museum
- Crypto-Gram Newsletter
- Cypherpunk -- A history
- Internet Engineering Task Force (IETF) Security Area
- An Open Specification for Pretty Good Privacy (openpgp)
- Common Authentication Technology (cat)
- IP Security Protocol (ipsec)
- One Time Password Authentication (otp)
- Public Key Infrastructure (X.509) (pkix)
- S/MIME Mail Security (smime)
- Simple Public Key Infrastructure (spki)
- Transport Layer Security (tls)
- Web Transaction Security (wts)
- Web Security (websec)
- XML Digital Signatures (xmldsig)
- Kerberos: The Network Authentication Protocol (MIT)
- The MIT Kerberos & Internet trust (MIT-KIT) Consortium (MIT)
- Peter Gutman's godzilla crypto tutorial
- RSA's Cryptography FAQ (v4.1, 2000)
- Interspersed in RSA's Public Key Cryptography Standards (PKCS) pages are a very good set of chapters about cryptography.
- Ron Rivest's "Cryptography and Security" Page
- "List of Cryptographers" from U.C. Berkeley
- Software:
- Wei Dai's Crypto++, a free C++ class library of cryptographic primitives
- Peter Gutman's cryptlib security toolkit
- A Perl implementation of RC4 (for academic but not production purposes) can be found at http://www.garykessler.net/software/index.html#RC4.
- A Perl program to decode Cisco type 7 passwords can be found at https://www.garykessler.net/software/index.html#cisco7.
And for a purely enjoyable fiction book that combines cryptography and history, check out Neal Stephenson's Cryptonomicon (published May 1999). You will also find in it a new secure crypto scheme based upon an ordinary deck of cards (ok, you need the jokers...) called the Solitaire Encryption Algorithm, developed by Bruce Schneier.
|
Finally, I am not in the clothing business although I did used to have an impressive t-shirt collection (over 350 and counting, at one point!). I still proudly wear the DES (well, actually the IDEA) encryption algorithm t-shirt from 2600 Magazine which, sadly, appears to be no longer available (left). (It was always ironic to me that The Hacker Quarterly got the algorithm wrong but...) A t-shirt with Adam Back's RSA Perl code can be found at http://www.cypherspace.org/~adam/uk-shirt.html (right). | 
|
APPENDIX A. SOME MATH NOTES
A number of readers over time have asked for some rudimentary background on a few of the less well-known mathematical functions mentioned in this paper. Although this is purposely not a mathematical treatise, some of the math functions mentioned here are essential to grasping how modern crypto functions work. To that end, some of the mathematical functions mentioned in this paper are defined in greater detail below.
A.1. The Boolean Logic Functions
George Boole, a mathematician and philosopher in the mid-1800s, invented a form of algebra with which to express logical arguments. Boolean algebra provides the basis for building electronic computers and microprocessor chips. Boole defined a bunch of primitive logical operations where there are one or two inputs and a single output depending upon the operation; the input and output are either TRUE or FALSE. The most elemental Boolean operations are:
- NOT (¬): The output value is the inverse of the input value (i.e., the output is TRUE if the input is false, FALSE if the input is true).
- AND (• or ∧): The output is TRUE if all inputs are true, otherwise FALSE. (E.g., "the sky is blue AND the world is flat" is FALSE while "the sky is blue AND security is a process" is TRUE.)
- OR (+ or ∨): The output is TRUE if either or both inputs are true, otherwise FALSE. (E.g., "the sky is blue OR the world is flat" is TRUE and "the sky is blue OR security is a process" is TRUE.)
- Exclusive OR (XOR, ⊕): The output is TRUE if exactly one of the inputs is TRUE, otherwise FALSE. (E.g., "the sky is blue XOR the world is flat" is TRUE while "the sky is blue XOR security is a process" is FALSE.)
The four Boolean functions are generally represented by the use of a truth tables; in computers, Boolean logic is implemented in logic gates. For design purposes, NOT has one input and the other three functions have two inputs (black); all have a single output (red). The logic diagrams appear below:
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
XOR is one of the fundamental mathematical operations used in cryptography (and many other applications). In an XOR operation, the output will be a 1 if exactly one input is a 1; otherwise, the output is 0. The real significance of this is to look at the "identity properties" of XOR. In particular, any value XORed with itself is 0 (i.e., x ⊕ x = 0) and any value XORed with 0 is just itself (i.e., x ⊕ 0 = x). Why does this matter? Well, if you take a plaintext string of 0s and 1s, and XOR it with a key string of 0s and 1s, you get a new jumbled string of 0s and 1s. If you then take that jumble and XOR it with the same key, you return to the original plaintext.
NOTE: Boolean truth tables usually show the inputs and output as a single bit because they are based on single bit inputs, namely, TRUE and FALSE. In addition, we tend to apply Boolean operations bit-by-bit. For convenience, I have created Boolean logic tables when operating on bytes.
A.2. The modulo Function
The modulo function is, simply, the remainder function. It is commonly used in programming and is critical to the operation of any mathematical function using digital computers.
To calculate X modulo Y (usually written X mod Y), you merely determine the remainder after removing all multiples of Y from X. Clearly, the value X mod Y will be in the range from 0 to Y-1.
Some examples should clear up any remaining confusion:
- 15 mod 7 = 1
- 25 mod 5 = 0
- 33 mod 12 = 9
- 203 mod 256 = 203
Modulo arithmetic is useful in crypto because it allows us to set the size of an operation and be sure that we will never get numbers that are too large. This is an important consideration when using digital computers.
A.3. Information Theory and Entropy
Information theory is the formal study of reliable transmission of information in the least amount of space or, in the vernacular of information theory, the fewest symbols. For purposes of digital communication, a symbol can be a byte (i.e., an eight-bit octet) or an even smaller unit of transmission.
The father of information theory is Bell Labs scientist and MIT professor Claude E. Shannon. His seminal paper, "A Mathematical Theory of Communication" (The Bell System Technical Journal, Vol. 27, pp. 379-423, 623-656, July, October, 1948), defined a field that has laid the mathematical foundation for so many things that we take for granted today, from data compression, data storage, data communication, and quantum computing to language processing, plagiarism detection and other linguistic analysis, and statistical modeling. Information theory also applies to cryptography, and a student of information theory and cryptography will most certainly want to see the International Association for Cryptologic Research's page on Shannon's 1945 paper, "A Mathematical Theory of Cryptography."
There are many everyday computer and communications applications that have been enabled by the formalization of information theory, such as:
- Lossless data compression, where the compressed data is an exact replication of the uncompressed source (e.g., PKZip, GIF, PNG, and WAV).
- Lossy data compression, where the compressed data can be used to reproduce the original uncompressed source within a certain threshold of accuracy (e.g., JPG and MP3).
- Coding theory, which describes the impact of bandwidth and noise on the capacity of data communication channels from modems to Digital Subscriber Line (DSL) services, why a CD or DVD with scratches on the surface can still be read, and codes used in error-correcting memory chips and forward error-correcting satellite communication systems.
One of the key concepts of information theory is that of entropy. In physics, entropy is a quantification of the disorder in a system; in information theory, entropy describes the uncertainty of a random variable or the randomness of an information symbol. As an example, consider a file that has been compressed using PKZip. The original file and the compressed file have the same information content but the smaller (i.e., compressed) file has more entropy because the content is stored in a smaller space (i.e., with fewer symbols) and each data unit has more randomness than in the uncompressed version. In fact, a perfect compression algorithm would result in compressed files with the maximum possible entropy; i.e., the files would contain the same number of 0s and 1s, and they would be distributed within the file in a totally unpredictable, random fashion.
As another example, consider the entropy of passwords (this text is taken from my paper, "Passwords — Strengths And Weaknesses," citing an example from Firewalls and Internet Security: Repelling the Wily Hacker by Cheswick & Bellovin [1994]):
Most Unix systems limit passwords to eight characters in length, or 64 bits. But Unix only uses the seven significant bits of each character as the encryption key, reducing the key size to 56 bits. But even this is not as good as it might appear because the 128 possible combinations of seven bits per character are not equally likely; users usually do not use control characters or non-alphanumeric characters in their passwords. In fact, most users only use lowercase letters in their passwords (and some password systems are case-insensitive, in any case). The bottom line is that ordinary English text of 8 letters has an information content of about 2.3 bits per letter, yielding an 18.4-bit key length for an 8-letter passwords composed of English words. Many people choose names as a password and this yields an even lower information content of about 7.8 bits for the entire 8-letter name. As phrases get longer, each letter only adds about 1.2 to 1.5 bits of information, meaning that a 16-letter password using words from an English phrase only yields a 19- to 24-bit key, not nearly what we might otherwise expect.
Encrypted files tend to have a great deal of randomness. This is why a compressed file can be encrypted but an encrypted file cannot be compressed; compression algorithms rely on redundancy and repetitive patterns in the source file and such syndromes do not appear in encrypted files.
Randomness is such an integral characteristic of encrypted files that an entropy test is often the basis for searching for encrypted files. Not all highly randomized files are encrypted, but the more random the contents of a file, the more likely that the file is encrypted. As an example, AccessData's Forensic Toolkit (FTK), software widely used in the computer forensics field, uses the following tests to detect encrypted files:
- Χ2 Error Percent: This distribution is calculated for a byte stream in a file; the value indicates how frequently a truly random number would exceed the calculated value.
- Entropy: Describes the information density (per Shannon) of a file in bits/character; as entropy approaches 8, there is more randomness.
- MCPI Error Percent: The Monte Carlo algorithm uses statistical techniques to approximate the value of π; a high error rate implies more randomness.
- Serial Correlation Coefficient: Indicates the amount to which each byte is an e-mail relies on the previous byte. A value close to 0 indicates randomness.
SIDEBAR: An 8-bit byte has 256 possible values. The entropy (E) of a binary file can be calculated using the following formula:
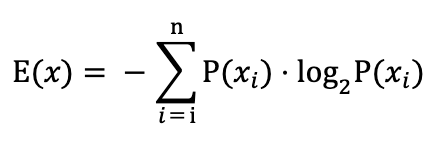
where n=256 and P(xi) is the probability of a byte in this file having the value i. A small Perl program to compute the entropy of a file can be found at entropy.zip.
Given this need for randomness, how do we ensure that crypto algorithms produce random numbers for high levels of entropy? Computers use random number generators (RNGs) for myriad purposes but computers cannot actually generate truly random sequences but, rather, sequences that have mostly random characteristics. To this end, computers use pseudorandom number generator (PRNG), aka deterministic random number generator, algorithms. NIST has a series of documents (SP 800-90: Random Bit Generators) that address this very issue:
- SP 800-90A: Recommendation for Random Number Generation Using Deterministic Random Bit Generators
- Draft SP 800-90 B: Recommendation for the Entropy Sources Used for Random Bit Generation
- Draft SP 800-90 C: Recommendation for Random Bit Generator (RBG) Constructions
The IETF's view of the randomness requirements for security can be found in RFC 4086. That paper notes several pitfalls when weak forms of entropy or traditional PRNG techniques are employed for purposes of security and cryptography. They also recommend the use of truly random hardware techniques and describe how existing systems can be used for these purposes. RFC 8937, produced by the Crypto Forum Research Group (CFRG), describes how security protocols can supplement their so-called "cryptographically secure" PRNG algorithms using long-term private keys.
SIDEBAR: While the purpose of this document is supposed to be tutorial in nature, I cannot totally ignore the disclosures of Edward Snowden in 2013 about NSA activities related to cryptography. One interesting set of disclosures is around deliberate weaknesses in the NIST PRNG standards at the behest of the NSA. NIST denies any such purposeful flaws but this will be evolving news over time. Interested readers might want to review "NSA encryption backdoor proof of concept published" (M. Lee), "Dual_EC_DRBG backdoor: a proof of concept" (A. Adamantiadis), or "Juniper Breach Mystery Starts to Clear With New Details on Hackers and U.S. Role" (J. Robertson).
Before thinking that this is too obscure to worry about, let me point out a field of study called kleptography, the "study of stealing information securely and subliminally" (see "The Dark Side of Cryptography: Kleptography in Black-Box Implementations"). Basically, this is a form of attack from within a cryptosystem itself. From that article comes this whimsical example: Imagine a cryptosystem (hardware or software) that generates PKC key pairs. The private key should remain exclusively within the system in order to prevent improper use and duplication. The public key, however, should be able to be freely and widely distributed since the private key cannot be derived from the public key, as described elsewhere in this document. But, now suppose that a cryptographic back door is embedded into the cryptosystem, allowing an attacker to access or derive the private key from the public key — such as weakening the key generation process at its heart by compromising the random number generators essential to creating strong key pairs. The potential negative impact is obvious.
Along these lines, another perspective of the Snowden disclosures relates to the impact on the world's most confidential data and critical infrastructures if governments are able to access encrypted communications. In July 2015, 14 esteemed cryptographers and computer scientists released a paper continuing the debate around cryptography and privacy. The paper, titled "Keys Under Doormats: Mandating insecurity by requiring government access to all data and communications," argues that government access to individual users' encrypted information will ultimately yield significant flaws in larger systems and infrastructures. Also check out the N.Y. Times article, "Security Experts Oppose Government Access to Encrypted Communication" (N. Perlroth).
Do not underestimate the importance of good random number generation to secure cryptography — and do not forget that an algorithm might be excellent but the implementation poor. Read, for example, "Millions of high-security crypto keys crippled by newly discovered flaw" (D. Goodin), which reported on a weakness in an RSA software library. Because RSA prime factorization arithmetic can be very complex on smart cards and other energy and memory constrained devices, the code for generating keys employed coding shortcuts. The result was that an attacker could calculate the private key from a vulnerable key-pair by only knowing the public key, which is totally anathema to the whole concept of public-key cryptography (i.e., the public key is supposed to be widely known without compromise of the private key). The vulnerability was due to the fact that the weakness was in the RNG and, therefore, a reduced level of randomness in the relationship between the private and public keys. This flaw, exposed in November 2017, had been present since at least 2012.
For readers interested in learning more about information theory, see the following sites:
- Wikipedia entry for Information Theory
- A Short Course in Information Theory (Eight lectures by David J.C. MacKay)
- Entropy and Information Theory by Gray (Revised 1st ed., 1991). In 2011, the second edition was published.
Finally, it is important to note that information theory is a continually evolving field. There is an area of research essentially questioning the "power" of entropy in determining the strength of a cryptosystem. An interesting paper about this is "Brute force searching, the typical set and Guesswork" by Christiansen, Duffy, du Pin Calmon, & Médard (2013 IEEE International Symposium on Information Theory); a relatively non-technical overview of that paper can be found at "Encryption is less secure than we hoped" by Gibbs (NetworkWorld, 08/16/2013). If you're going this far, also take a look at "Entropy as a Service: Unlocking Cryptography's Full Potential" (A. Vassilev & R. Staples, September 2016, Computer, 49(9), pp. 98-102).
A.4. Cryptography in the Pre-Computer Era
This paper purposely focuses on cryptography terms, concepts, and schemes used in digital devices and is not a treatise of the whole field. No mention is made here about pre-computerized crypto schemes, the difference between a substitution and transposition cipher, cryptanalysis, or other history, nor is there a lot of theory presented here. That said, the history and evolution of cryptography is really interesting and readers should check out some of the books in the References and Further Reading section above.
There are also several excellent Web sites that provide detailed information about the history of cryptographic methods, such as:
Crypto Lab is a series of blog-like posts describing various encryption methods. The entire set of pages for offline viewing can be found at GitHub.
Crypto Programs is an online collection of more than 50 classical substitution and transposition encryption schemes.
The CrypTool Portal is designed to raise awareness about cryptography and contains a collection of free software with which to experiment with a variety of ciphers.
The Learn Cryptography Encryption page has a lot of information about classical and historic encryption methods, as well as pages about cryptanalysis, cryptocurrency, hash functions, and more.
The MultiWingSpan Ciphers page discusses a dozen or so manual encryption schemes as a setup to a series of programming assignments.
The Practical Cryptography Ciphers page provides history, math, and sample implementations of a couple dozen manual encryption codes. Other pages discuss cryptanalysis and hash functions.
Finally, my software page contains a Perl program that implements several manual crypto schemes, including Caesar, Atbash, Vigenere Square, Beaufort, Myszkowski Transpostition, and ADFGVX ciphers.
A.5. A Short Introduction to Groups
Without a lot of explanation, I have made passing reference a few times in this paper to the concept of a group. In this section, I will give a very light introduction to some group theory. In mathematics, a group refers to a set of elements that can be combined by some operation. An important requirement is that when any two elements within the group are combined using the operation, the result is another element that is a member of the group. In that case, the group is said to be closed under that operation.
So, by way of example, the set of positive integers ({1...∞}) is closed under addition because any two members of this group, when added, yields another member of the group. As a simple example, 3 and 18 are both members of the set of positive integers, as is their sum, 21. The sets of non-negative integers ({0...∞}) and all integers ({-∞...∞}, often denoted Z) are also closed under addition.
These three groups are also closed under multiplication because, again, if you start with any two members of the set, their product is also a member of the set (e.g., 3 × 18 = 54).
As it happens, these three groups are not all closed under subtraction. Consider that 3 - 18 = -15. This shows that Z is closed under subtraction, but the subsets of positive and non-negative integers are not.
Finally, none of these sets are closed under division. Continuing with our friends, 3 and 18, we find that 3 ÷ 18 = 1/6 which is not a member of any set or subset of integers.
So, continuing down this path just a bit more, let's take a look at the set of rational numbers. Rational numbers, usually denoted Q, are numbers that can be expressed as a fraction p/q, where p and q are integers and q≠0. The set of rational numbers is closed under division. As an example, consider two rational numbers, 5/6 and 11/12; dividing (5/6)/(11/12) yields a new rational number, namely 60/66 which can be reduced to 10/11. Irrational numbers, such as e, π, and √2, cannot be expressed as a simple fraction.
APPENDIX B. ACRONYMS AND ABBREVIATIONS
| 3DES | Triple DES |
| AES | Advanced Encryption Standard |
| AH | IPsec Authentication Header |
| ANSI | American National Standards Institute |
| ARPANET | Advanced Research Projects Agency |
| ASCII | American Standard Code for Information Interchange |
| ASIC | Application-specific integrated circuit |
| CA | Certificate authority |
| CBC | Cipher block chaining |
| CHAP | Challenge-Handshake Authentication Protocol |
| CPU | Central processing unit |
| CRYPTEC | Cryptography Research and Evaluation Committees |
| DES | Data Encryption Standard |
| DSA | Digital Signature Algorithm |
| DSS | Digital Signature Standard |
| ECC | Elliptical Curve Cryptography |
| EFF | Electronic Frontier Foundation |
| EFS | Encrypting File System |
| EPIC | Electronic Privacy Information Center |
| ESP | IPsec Encapsulating Security Payload |
| FIPS | Federal Information Processing Standard |
| FPGA | Field-programmable gate array |
| FTP | File Transfer Protocol |
| GCHQ | Government Communications Headquarters |
| GPG | GNU Privacy Guard |
| GUI | Graphical user interface |
| HMAC | Hash-based or Keyed-Hash Message Authentication Code |
| HTTP | Hypertext Transfer Protocol |
| HTTPS | Hypertext Transfer Protocol over SSL |
| IBE | Identify-Based Encryption |
| IDEA | International Data Encryption Algorithm |
| IEEE | Institute of Electrical and Electronics Engineers |
| IETF | Internet Engineering Task Force |
| IKE | IPsec Internet Key Exchange |
| IP | Internet Protocol or Initial permutation |
| IPsec | IP Security |
| IPv4/IPv6 | Internet Protocol version 4/version 6 |
| ISAKMP | IPsec Internet Security Association and Key Management Protocol |
| KB | kilobyte; 1,024 (210) bytes |
| MAC | Message Authentication Code |
| MDn | Message Digest n (MD2, MD4, MD5) |
| MIME | Multipurpose Internet Mail Extensions |
| NBS | National Bureau of Standards |
| NESSIE | New European Schemes for Signatures, Integrity and Encryption |
| NIST | National Institute of Standards and Technology |
| NSA | National Security Agency |
| PC | Personal computer |
| PCMCIA | Personal Computer Memory Card International Association |
| PDA | Personal digital assistant |
| PEM | Privacy-Enhanced Mail |
| PGP | Pretty Good Privacy |
| PKC | Public key cryptography |
| PKCS | Public Key Cryptography Standards |
| PKI | Public key infrastructure |
| RAM | Random-access memory |
| RCn | Ron's Code n or Rivest Cipher n (RC2, RC4, RC5, RC6) |
| RFC | Request for Comments |
| RFID | Radio-frequency identification |
| RSA | Rivest, Shamir, Adleman |
| S/MIME | Secure Multipurpose Internet Mail Extensions |
| SA | IPsec Security Association |
| SCUBA | Self-contained underwater breathing apparatus |
| SETI | Search for extraterrestrial intelligence |
| SHA | Secure Hash Algorithm |
| SKC | Secret key cryptography |
| SSL | Secure Sockets Layer |
| TCP | Transmission Control Protocol |
| TLS | Transaction Layer Security |
| UDP | User Datagram Protocol |
| URL | Uniform Resource Locator |
| USB | Universal Serial Bus |
| XOR | Exclusive OR |
ABOUT THE AUTHOR
Gary C. Kessler, Ph.D., CCE, CISSP, is the president and janitor of Gary Kessler Associates, a consulting, research, and training firm specializing in computer and network security (with a focus on maritime cybersecurity), computer forensics, and TCP/IP networking. He has written over 75 papers, articles, and book chapters for industry publications, is co-author of ISDN, 4th. edition (McGraw-Hill, 1998), a past editor-in-chief of the Journal of Digital Forensics, Security and Law, and co-author of Maritime Cybersecurity: A Guide for Leaders and Managers, 2/e (2022). Gary retired as Professor of Cybersecurity at Embry-Riddle Aeronautical University in Daytona Beach, Florida, and is an Adjunct Professor at Edith Cowan University in Perth, Western Australia. Gary was formerly an Associate Professor and Program Director of the M.S. in Information Assurance program at Norwich University in Northfield, Vermont, and a member of the Vermont Internet Crimes Against Children (ICAC) Task Force; he started the M.S. in Digital Investigation Management and undergraduate Computer & Digital Forensics programs at Champlain College in Burlington, Vermont. Gary's e-mail address is gck@garykessler.net and his PGP public key can be found at https://www.garykessler.net/pubkey.html. Gary is also a SCUBA instructor and U.S. Coast Guard licensed captain.
ACKNOWLEDGEMENTS
This section was introduced late in the life of this paper and so I apologize to any of you who have made helpful comments that remain unacknowledged. If you did make comments that I adopted — from catching typographical or factual errors to suggesting a new resource or topic — and I have failed to recognize you, please remind me!
Thanks are offered to Steve Bellovin, Sitaram Chamarty, DidiSoft, Bernhard Esslinger (and his students at the University of Siegen, Germany, contributors to the CrypTool project), William R. Godwin, Craig Heilman, Luveh Keraph, Robert Litts, Hugh Macdonald, Douglas P. McNutt, Marcin Olak, Josh Silman, Barry Steyn, and Miles Wolbe.

